Hình thoi là một trong những hình gặp rất nhiều trong những bài toán về hình học trong suốt quy trình học tập của chúng ta. Cho nên vì vậy các bạn cần phải nắm được định nghĩa, dấu hiệu nhận biết với tính chất hình thoi thì mới những thể vận dụng giải bài tập dễ dàng.
Bạn đang xem: Đặc điểm hình thoi
Hình thoi là gì?
Hình thoi là tứ giác gồm 4 lân cận bằng nhau. Hình thoi là hình bình hành gồm hai cạnh kề đều nhau hay hình bình hành có hai đường chéo cánh vuông góc cùng với nhau.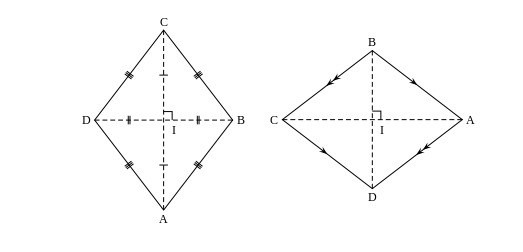
Tính hóa học hình thoi
Trong hình thoi:
Các góc đối nhau bằng nhau.Hai đường chéo cánh vuông góc với nhau và giảm nhau tại trung điểm của mỗi đường.Hai đường chéo cánh là những đường phân giác của những góc của hình thoi.Hình thoi có tất cả tính hóa học của hình bình hành. Đó là: các cạnh đối tuy nhiên song và bởi nhau, các góc đối bằng nhau, hai đường chéo cánh cắt nhau trên trung điểm mỗi đường.Dấu hiệu nhận thấy hình thoi
Hình tứ giác đặc biệt
Tứ giác gồm bốn cạnh đều nhau là hình thoi.Tứ giác tất cả 2 đường chéo cánh là đường trung trực của nhau là hình thoi.Tứ giác gồm 2 đường chéo cánh là con đường phân giác của cả bốn góc là hình thoi.Hình bình hành đặc biệt
Hình thoi là 1 dạng đặc biệt của một hình bình hành vị nó có đầy đủ tính chất của hình bình hành và còn tồn tại một số đặc thù khác:Hình bình hành bao gồm hai cạnh kề bằng nhau là hình thoi.Hình bình hành tất cả hai đường chéo cánh vuông góc cùng nhau là hình thoi.Hình bình hành bao gồm một đường chéo là con đường phân giác của một góc là hình thoi.Bài tập chứng minh về hình thoi
Dưới đó là 4 cách chứng minh hình thoi các chúng ta cũng có thể tham khảo
Cách 1: Tứ giác có bốn cạnh bằng nhau
Ví dụ: mang đến hình chữ nhật ABCD có những trung điểm của bốn cạnh theo lần lượt là M, N, P, Q. Minh chứng rằng những trung đặc điểm đó là các đỉnh của hình thoi.
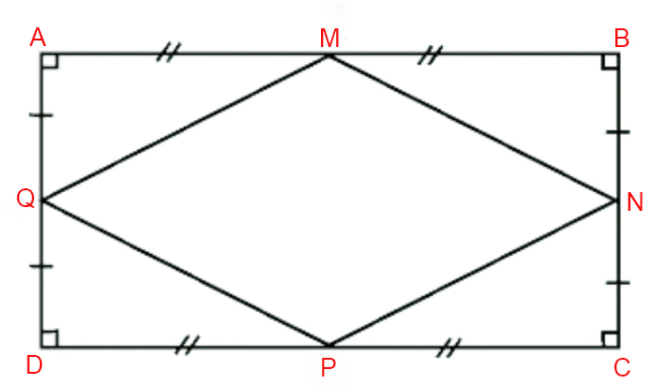
Lời giải:
Xét ΔABD tất cả M với Q theo thứ tự là trung điểm của AB cùng AD.
⇒ MQ là con đường trung bình của ΔABD.
⇒ MQ = ½ BD (1).
Chứng minh tương tự ta có: MN = ½ AC; NP = ½ BD; PQ = ½ AC (2).
Vì ABCD là hình chữ nhật đề nghị AC = BD (3).
Từ (1), (2) và (3), ta suy ra MQ = MN = NP = PQ.
⇒ Tứ giác MNPQ là hình thoi do gồm bốn cạnh bằng nhau.
Cách 2: Tứ giác gồm 2 đường chéo là đường trung trực của nhau
Ví dụ: đến hình bình hành ABCD bao gồm AB = AC. Kéo dãn trung con đường AE của ΔABC và lấy EA = EF. Chứng minh tứ giác ABFC là hình thoi.
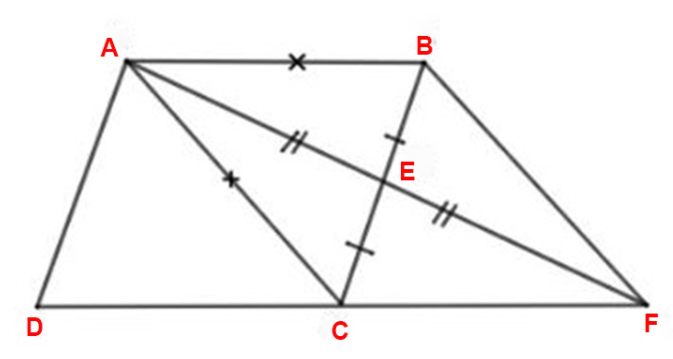
Ta có:
ΔABC cân tại A gồm trung tuyến AE.
⇒ AE là con đường trung trực của BC.
⇒ Tứ giác ABFC là hình thoi do gồm 2 đường chéo là mặt đường trung trực của nhau.
Xem thêm: Review Vương Quốc Dục Cảm - In The Realm Of The Senses 1976
Cách 3: Hình bình hành gồm hai cạnh kề bởi nhau
Ví dụ: mang đến tam giác ABC, lấy các điểm D, E theo trang bị tự trên các cạnh AB, AC sao cho BD = CE. Gọi M, P, Q, O lần lượt là trung điểm của BE, CD, DE, BC. Chứng minh rằng: MQPO là hình thoi.
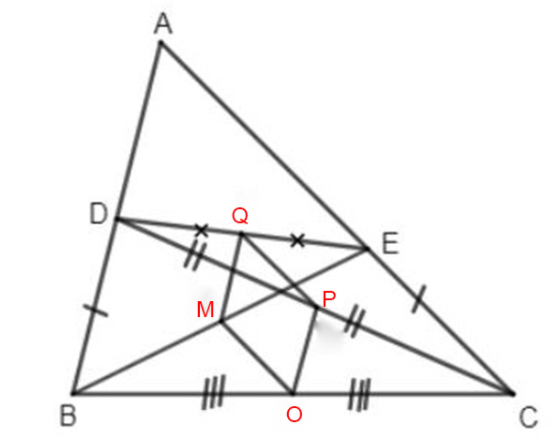
Lời giải
M là trung điểm của BE cùng Q là trung điểm của DE.
⇒ MQ là con đường trung bình của ΔBDE.
⇒ MQ // BD với MQ = ½ BD.
Chứng minh tương tự, ta có:
PO // BD với PO = ½ BD.
Do có MQ // PO cùng MQ = PO phải tứ giác MQPO là hình bình hành (4).
Tương tự, ta có: QP là con đường trung bình của ΔCDE.
⇒ QP = ½ CE nhưng CE = BD (giả thiết) => QM = QP (5).
Từ (4) cùng (5) ⇒ Tứ giác MQPO là hình thoi vì chưng là hình bình hành gồm hai cạnh kề bằng nhau.
Cách 4: Hình bình hành có hai đường chéo vuông góc
Ví dụ: hotline O là giao điểm nhị đường chéo cánh của hình bình hành ABCD. Chứng tỏ rằng giao điểm những đường phân giác trong của các tam giác ΔAOB; ΔBOC; ΔCOD với ΔDOA là đỉnh của một hình thoi.
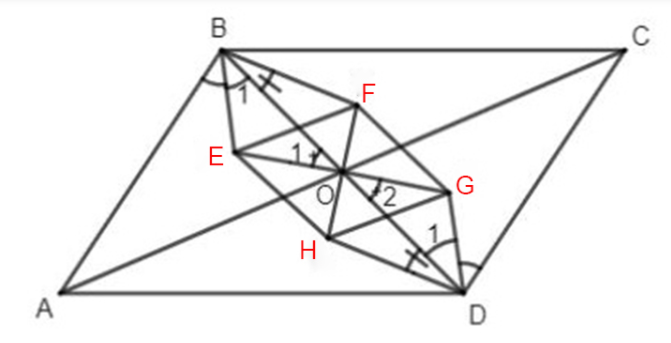
Lời giải:
Gọi E, F, G, H thứu tự là giao điểm các phân giác trong của các tam giác AOB, BOC, COD và DOA.
Do O là giao điểm nhị đường chéo cánh AC cùng BD của hình bình hành ABCD đề xuất OA = OC và OB = OD.
Xét ΔBEO với ΔDGO có:
Góc B1 = D1 và Góc O1 = O2 (đối đỉnh) cùng OB = OD (giả thiết).
=> ΔBEO = ΔDGO (góc cạnh góc).
=> OE = OG và những điểm E, O, G thẳng sản phẩm (6).
Chứng minh tương tự: OF = OH cùng F, O, H thẳng sản phẩm (7)
Từ (6) và (7) Suy ra: Tứ giác EFGH là hình bình hành do các đường chéo cánh cắt nhau trên trung điểm từng đường. (8)
Mặt không giống ta lại sở hữu OE ⊥ OF (là con đường phân giác của hai góc kề bù). (9)
Từ (8) và (9) suy ra: EFGH là hình thoi bởi vì là hình bình hành có hai đường chéo vuông góc.
Hy vọng cùng với những tin tức mà cửa hàng chúng tôi vừa share có thể giúp các bạn nhớ được định nghĩa, lốt hiệu phân biệt và tính chất hình thoi nhé














