(suacuacuon.edu.vn Giáo Dục) - Để giải được các bài toán về đường cao tam giác vuông cân, việc trước tiên các bạn cần phải nắm vững vàng được đặc điểm và bí quyết tính con đường cao tam giác vuông cân. Để tra cứu hiểu cụ thể về kiến thức này mời mọi fan cùng theo dõi bài xích viết.
Bạn đang xem: Đường cao của tam giác vuông
Đường cao vào tam giác vuông cân nặng là phần kiến thức mà ta sẽ chạm chán thường xuyên vào suốt quy trình học môn Toán trường đoản cú lớp 7 đến lớp 12. Vậy tính chất đặc trưng của nó là gì với làm ráng nào để tính được độ dài đường cao tam giác vuông cân? nội dung bài viết sau trên đây suacuacuon.edu.vn Giáo Dục sẽ reviews tới các em một vài tính chất quan trọng đặc biệt cùng với công thức tính độ dài mặt đường cao tam giác vuông cân.
1. Đường cao trong tam giác vuông cân nặng là gì?
Trong tam giác MNP vuông cân tại M, đoạn trực tiếp vuông góc kẻ tự đỉnh M mang đến đường thẳng đựng cạnh NP được hotline là con đường cao của tam giác vuông cân nặng MNP. Cụ thể trong hình vẽ bên dưới đây, ta nói đoạn thẳng MH là con đường cao xuất phát từ đỉnh M của của tam giác vuông cân nặng MNP.
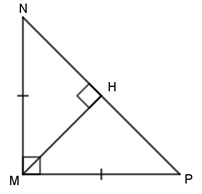
2. Tính chất đường cao vào tam giác vuông cân
Trong tam giác MNP vuông cân nặng tại M, có đường cao MH. Ta tất cả các tính chất như sau:
Tam giác vuông MHN bởi tam giác vuông MHP;Độ dài của nhì đoạn thẳng NH cùng đoạn trực tiếp PH là đều nhau hay điểm H là trung điểm của đoạn thẳng NP. Khi đó, đường cao MH đó là đường trung tuyến của tam giác vuông cân nặng MNP;. Lúc đó, mặt đường cao MH chính là đường phân giác góc NMP của tam giác vuông cân MNP;Hai cạnh góc vuông NM cùng PM là mặt đường cao khởi đầu từ đỉnh N và p. Tương ứng của tam giác vuông cân nặng MNP.
3. Chứng minh các đặc điểm đường cao tam giác vuông cân
(1) bởi vì tam giác MNP là tam giác vuông cân tại M, suy ra .Lại bao gồm MH vuông góc cùng với NP, buộc phải ta có .
Trong tam giác vuông MHN có:
(tổng cha góc trong một tam giác).
Suy ra .
Tương tự vào tam giác vuông MHP có:
(tổng tía góc vào một tam giác).
Suy ra .
Do kia ta có .
Xét tam giác vuông MHN cùng tam giác vuông MHP có:
+
+
+
Do kia ta được: Tam giác vuông MHN bằng tam giác vuông MHP (g.g.g).
(2) Theo đặc điểm (1), ta có: Tam giác vuông MHN bởi tam giác vuông MHP.
Suy ra NH = PH hay điểm H là trung điểm của đoạn trực tiếp NP.
Khi đó, con đường cao MH đó là đường trung tuyến đường của tam giác vuông cân nặng MNP.
(3) phụ thuộc vào phần minh chứng của đặc thù (1), ta có: .
Khi đó, con đường cao MH chính là đường phân giác góc NMP của tam giác vuông cân nặng MNP.
(4) Do NM và PM là nhì cạnh góc vuông của tam giác MNP.
Suy ra cạnh NM vuông góc với cạnh MP cùng cạnh PM vuông góc với cạnh MN.
Khi đó, NM và PM là đường cao xuất phát điểm từ đỉnh N và phường tương ứng của tam giác vuông cân nặng MNP.
4. Phương pháp tính mặt đường cao tam giác vuông cân
Trong tam giác MNP vuông cân nặng tại M, bao gồm đường cao MH. Lúc đó, độ dài con đường cao MH vào tam giác vuông cân nặng chính bởi một nửa độ dài cạnh NP tuyệt MH = NP.
Cách tính con đường cao tam giác vuông cânChứng minh
Trong tam giác MHN có: (theo minh chứng tính hóa học 1).
Suy ra tam giác MHN cân tại H tuyệt NH = MH.
Trong tam giác MHP có: (theo chứng minh tính hóa học 1).
Suy ra tam giác MHP cân tại H giỏi PH = MH.
Mà NH = HP = NP (theo tính chất 2).
Khi đó, ta được MH = NP.
5. Một trong những dạng toán thường chạm mặt liên quan con đường cao tam giác vuông cân
5.1. Dạng 1: bài bác tập bệnh minh
*Phương pháp giải:
Muốn chứng tỏ một điều nào đấy theo yêu mong của bài toán, ta sẽ áp dụng các đặc điểm và cách làm tính độ lâu năm của con đường cao trong một tam giác vuông cân đã trình bày ở bên trên vào để xử lý bài toán đó.
Xem thêm: Học Cách Dạy Trẻ Lớp 1 Tính Nhẩm Lớp 1 Tính Nhẩm Dễ DàNg DàNh Cho Phhs
Ví dụ 1. Mang đến tam giác MNP vuông cân nặng tại M, bao gồm đường cao MH. Kẻ đoạn trực tiếp HK vuông góc với cạnh MP tại điểm K. Minh chứng HK = NM.
Lời giải

Vì MH là con đường cao tam giác vuông cân MNP, phải theo tính chất 2 và công thức tính độ dài đường cao MH ta có: MH = HP = NP.
Lại gồm MH vuông góc cùng với NP bắt buộc .
Do kia tam giác MHP là tam giác vuông cân tại H.
Xét tam giác MHP vuông cân nặng tại H bao gồm HK là con đường cao xuất phát điểm từ đỉnh H.
Suy ra HK = MP (theo phương pháp tính độ dài đường cao tam giác vuông cân).
Mà MP = MN (tam giác MNP vuông cân tại M).
Do đó, ta suy ra HK = MN.
Vậy HK = NM.
5.2. Dạng 2: Tính độ dài đường cao tam giác vuông cân
*Phương pháp giải:
Ta áp dụng công thức tính độ dài đường cao tam giác vuông cân nặng đã trình bày ở trên.
Ví dụ 2. đến tam giác MNP vuông cân nặng tại M, có đường cao MH. Biết độ dài cạnh NP = 6 cm. Hãy tính độ dài đường cao MH.
Lời giải
Vì MH là con đường cao tam giác vuông cân MNP, phải theo phương pháp tính độ dài mặt đường cao ta có:
MH = NP = . 6 = 3 (cm)
Vậy mặt đường cao MH tất cả độ dài bằng 3 cm.
6. Một vài bài tập áp dụng đường cao tam giác vuông cân
Bài 1. cho tam giác HKT vuông cân nặng tại H bao gồm đường cao HR. Biết độ dài cạnh KT = 16 cm. Độ dài con đường cao HR là:
46816ĐÁP ÁN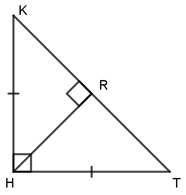
Vì HR là con đường cao tam giác vuông cân nặng HKT, yêu cầu theo công thức tính độ dài con đường cao ta có:
HR = KT = . 16 = 8 (cm)
Vậy con đường cao HR có độ dài bằng 8 cm.
Chọn lời giải C.
Bài 2. đến tam giác MNP vuông cân tại M, gồm đường cao MH. Hotline I là trung điểm của đoạn thẳng MN, nối p với I cắt đoạn thẳng MH tại J. Chứng minh MJ = MH.
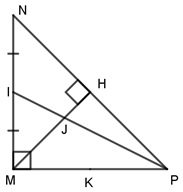
Vì I là trung điểm của MN, cần PI là mặt đường trung con đường kẻ tự đỉnh p. Của tam giác MNP.
Do MH là mặt đường cao của tam giác vuông cân MNP, theo tính chất 2 ta có MH đó là đường trung tuyến.
Ta bao gồm J là giao điểm của hai tuyến phố trung tuyến MH và PI, nên suy ra J là trọng tâm của tam giác MNP.
Theo tính chất ba đường trung tuyến của một tam giác ta được:
MJ = MH.
Bài 3. cho tam giác MNP vuông cân nặng tại M, gồm đường cao MH. Biết độ lâu năm hai cạnh MN = MP = 2 cm. Hãy tính độ dài đường cao MH.
ĐÁP ÁNXét tam giác MNP vuông trên M có:
MN2 + MP2 = NP2 (định lý Pi – ta – go).
Suy ra NP2 = 22 + 22 = 8 tuyệt NP = (cm).
Vì MH là con đường cao tam giác vuông cân MNP, phải theo bí quyết tính độ dài mặt đường cao ta có:
MH = NP = . = (cm)
Vậy mặt đường cao MH tất cả độ dài bằng cm.
Qua nội dung bài viết này mong những em nắm rõ hơn về các đặc điểm của mặt đường cao tam giác vuông cân, đồng thời dựa vào công thức đã nêu những em có thể tính được độ dài đường cao này.














