Nửa tam giác gần như là gì? Nêu những tính chất nửa tam giác đều. Trong bài viết này suacuacuon.edu.vn giáo dục sẽ đề cập cho định nghĩa, bí quyết tính, các đặc thù cơ bản và cách chứng tỏ nửa tam giác đều.
Bạn đang xem: Tính chất tam giác đều
Ở bài học trước bọn họ đã khám phá về tam giác đều. Vậy nửa tam giác đều là hình gì? cùng nửa tam giác đều có những đặc thù gì? Để tính độ dài các cạnh trong nửa tam giác rất nhiều ta làm cố kỉnh nào? Vậy để nắm rõ hơn về nửa tam giác đều bọn họ cùng nhau kiếm tìm hiểu bài viết này nhé.
1. Ôn tập về tam giác đều
1.1. Định nghĩa
Một tam giác được điện thoại tư vấn là tam giác phần lớn khi tam giác đó có ba cạnh bởi nhau.
1.2. Tính chất
Nếu tam giác MNK đều thì tam giác MNK gồm các tính chất sau:
- tía cạnh bởi nhau: MN = MK = NK
- ba góc cân nhau và bởi 60°: .
2. Nửa tam giác đều là gì?
Định nghĩa nửa tam giác đều: đến tam giác MNK đều, từ M kẻ MH vuông góc cùng với NK. Lúc đó, đường cao MH đã phân tách tam giác số đông MNK thành nhì tam giác vuông MHK với tam giác vuông MHN bởi nhau. Và hai tam giác MHK cùng tam giác MHN có đặc điểm như vậy được gọi là nửa tam giác đều.
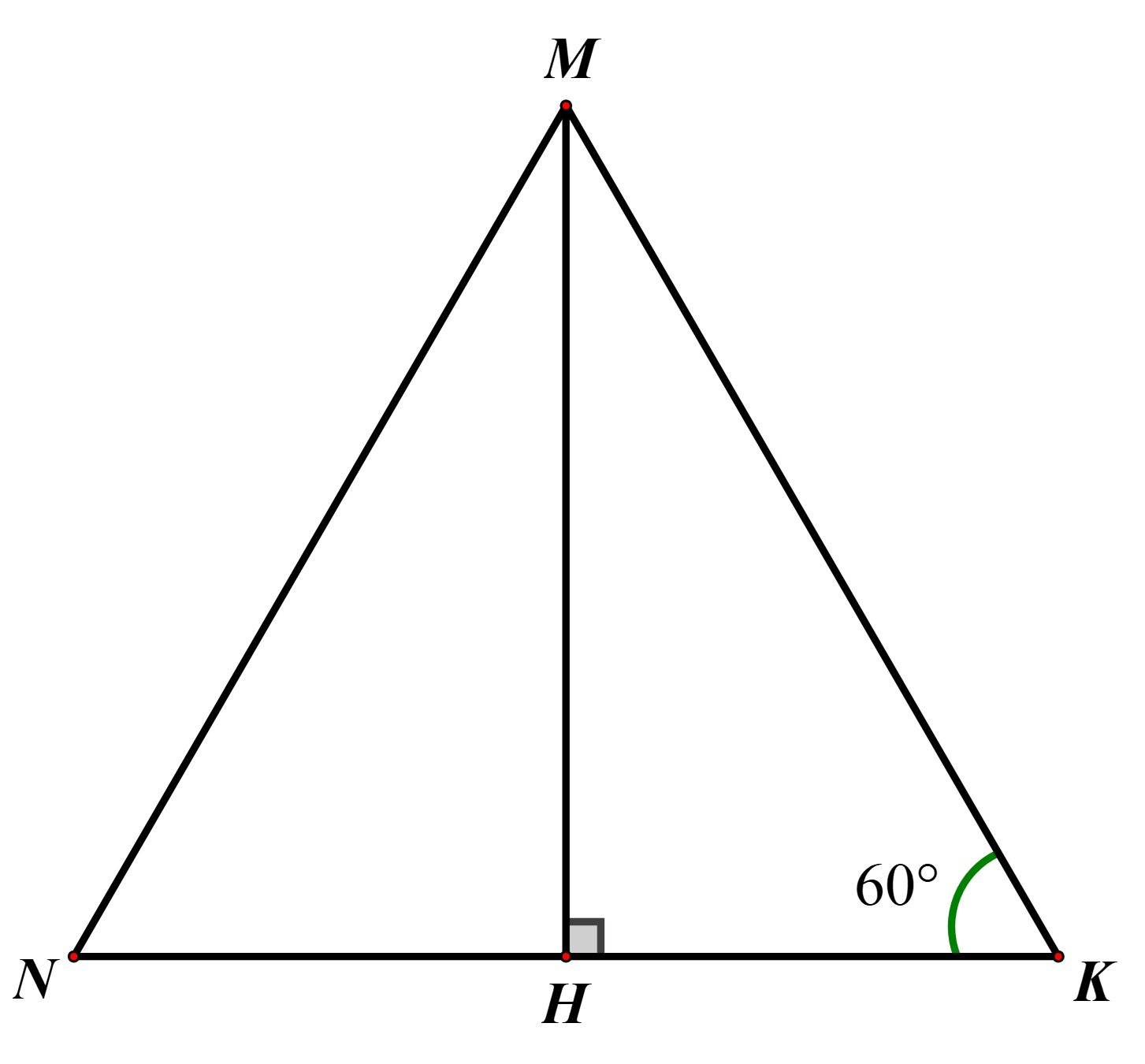
Qua đó, ta rút ra được định nghĩa: Nửa tam giác đều là một trong tam giác vuông có một góc nhọn bằng 60° hoặc một góc nhọn bởi 30°.
Lưu ý: Với mỗi đỉnh của tam giác phần đa ta gồm thể phân thành hai nửa tam giác đều bởi nhau.
3. đặc thù nửa tam giác đều
Nếu một tam giác là nửa tam giác phần đa thì tam giác đó gồm các tính chất sau:
- các góc nhọn tất cả số đo là 60° với 30°.
- Cạnh góc vuông đối lập với góc 30° gồm độ dài bằng nửa cạnh huyền.
Điều này ta hoàn toàn có thể dễ dàng minh chứng được qua lấy một ví dụ sau đây:
Ví dụ: Cho tam giác đầy đủ HMO, trường đoản cú H kẻ HK vuông góc với MO (K nằm trong MO).
a) Tính số đo góc MHK.
b) chứng tỏ rằng: KM bao gồm độ dài bằng nửa cạnh HM.
Giải.

a) Tam giác HMO hồ hết suy ra .
Tam giác HKM vuông tại K (HK ⊥ OM)
Suy ra
Nên
b) Tam giác HMO đều có HK là đường cao
⇒ HK đồng thời là con đường trung tuyến
⇒ K là trung điểm của OM
⇒ .
Mà OM = HM (vì tam giác HMO đều)
Vậy .
4. Tính độ dài những cạnh của nửa tam giác đều
Giả sử tam giác DEG là nửa tam giác đều phải sở hữu cạnh bởi a (như hình vẽ). lúc ấy ta trọn vẹn tính được độ dài các cạnh vào tam giác DEG.

+ Theo đặc thù của nửa tam giác đều, ta tất cả cạnh .
+ Tam giác DEG vuông trên D, vận dụng định lý Pytago ta có: .
Suy ra
Nên
Khi hiểu rằng độ dài các cạnh của nửa tam giác đều, họ sẽ tính được chu vi và diện tích của nửa tam giác đều.
+ Chu vi của tam giác DEG là: DE + DG + EG = .
+ diện tích của tam giác DEG là: .
Như vậy, nếu tam giác đều phải có độ dài cạnh bởi a thì công thức tính nửa tam giác đều đó là:
• Chu vi nửa tam giác đều: .
• diện tích nửa tam giác đều: .
5. Bài xích tập về nửa tam giác đều
5.1. Bài bác tập trắc nghiệm
*Phương pháp giải:Thông thường các bài tập trắc nghiệm làm việc dạng này liên quan đến các câu hỏi lý thuyết về nửa tam giác đều. Những em áp dụng khái niệm, tính chất, dấu hiệu nhận ra nửa tam giác phần đông để hoàn toàn có thể làm tốt dạng này.
Câu 1:Chọn câu trả lời đúng. Nửa tam giác đềulà:
A. Tam giác có bố cạnh đều bởi nhau.
B. Tam giác được phân chia ra bởi một mặt đường thẳng ngẫu nhiên của tam giác đều.
C. Tam giác vuông bao gồm một góc nhọn bằng 60°.
D. Tam giác tất cả hai góc cân nhau và cùng bằng 30°
ĐÁP ÁNTheo định nghĩa nửa tam giác đều, chọn đáp án C.
Câu 2.Chọn câu trả lời đúng.Cho tam giác RST vuông trên S gồm góc R= 30°. Lúc đó tam giác RST còn gọi là:
A. Tam giác cân
B. Nửa tam giác đều
C. Tam giác vuông cân
D. Tam giác cân
ĐÁP ÁNChọn đáp án B. Xem thêm: Những Bài Hát Có Hợp Âm Happy Birthday Ukulele, Happy Birthday By Misc Traditional
Tam giác RST vuông tại S có góc R= 30°. Khi đó tam giác RST có cách gọi khác là nửa tam giác đều.
Câu 3.Chọn câu vấn đáp đúng. Nửa tam giác đều có số đo tía góc lần lượt là:
A. 45°, 45°, 90°.
B. 60°, 60°, 60°.
C. 30°, 30°, 120°.
D. 30°, 60°, 90°.
ĐÁP ÁNChọn đáp án D.
Vì nửa tam giác mọi là tam giác vuông có một góc nhọn bởi 60° yêu cầu số đo cha góc vào nửa tam giác các lần lượt là: 30°, 60°, 90°.
Câu 4. Chọn câu trả lời đúng. Mang lại tam giác đều sở hữu cạnh 4 cm, khi đó diện tích của một phần tam giác hầu hết đó là:
A. S = 2 cm2.
B. S = cm2.
C. S = cm2.
D. S = cm2.
ĐÁP ÁNChọn lời giải C.
Dựa vào bí quyết tính cấp tốc đã nêu sống mục 4 diện tích nửa tam giác đông đảo là: .
Thay a = 4 centimet vào bí quyết ta có diện tích cần tìm là: cm2.
5.2. Bài tập tự luận
*Phương pháp giải. Các bài xích tập trường đoản cú luận ngơi nghỉ dạng này hay là những bài tập chứng minh nửa tam giác hầu như và tính độ dài các cạnh, những góc của nửa tam giác đều. Để chứng tỏ một tam giác là nửa tam giác đều, ta có thể chứng tỏ theo các cách sau:
Chứng minh tam giác vuông bao gồm một góc nhọn bởi 60°.Chứng minh tam giác vuông có một góc nhọn bằng 30°.Chứng minh tam giác vuông gồm một cạnh góc vuông tất cả độ dài bởi nửa cạnh huyền.Bài tập.Cho tam giác có các yếu tố sau, trong những tam giác kia tam giác làm sao là nửa tam giác đều?
a) Tam giác ABC gồm AB = 4cm, BC = 5cm, AC = 3cm.
b) Tam giác EGH vuông tại G tất cả .
c) Tam giác MNF tất cả MN = 4 cm, NF = cm, MF = 8 cm.
d) Tam giác RSK vuông trên S gồm RK = 16 cm, SR = 8 cm.
ĐÁP ÁNa) Tam giác ABC có:
BC2 = 52 = 25
AB2 + AC2 = 42 + 32 = 16 + 9 = 25
Suy ra BC2 = AB2 + AC2
Nên tam giác ABC là tam giác vuông tại A.
Khi kia hai cạnh góc vuông là AB = 4cm, AC = 3cm. Cạnh huyền BC = 5 cm.
Vì tam giác vuông ABC không tồn tại cạnh góc vuông nào bằng nửa cạnh huyền nên tam giác ABC không phải là nửa tam giác đều.
b) Tam giác EGH vuông tại G tất cả đề nghị tam giác EGH là tam giác vuông có một góc nhọn bằng 60°
Vậy tam giác EGH là nửa tam giác đều.
c) Tam giác MNF có:
MF2 = 82 = 64
MN2 + NF2 =
Suy ra MF2 = MN2 + NF2
Nên tam giác MNF là tam giác vuông tại N.
Khi kia ta có cạnh góc vuông MN bằng một nửa cạnh huyền MF (vì MN= 4cm, MF = 8 cm)
Vậy tam giác MNF là nửa tam giác đều.
d) Tam giác RSK vuông trên S buộc phải RK là cạnh huyền, SR là cạnh góc vuông.
Mà RK = 16 cm, SR = 8 cm buộc phải cạnh SR bằng nửa cạnh RK.
Vậy tam giác RSK là nửa tam giác đều.
Hy vọng nội dung bài viết này sẽ giúp các em phát âm và vận dụng được con kiến thức để làm tốt các bài tập tương quan đến nửa tam giác đa số và những bài tập minh chứng nửa tam giác đều.














