Tìm gọi những kiến thức hữu ích về Tích Chất và Cách Tính Đường Cao Tam Giác Đều, Vuông, cân nặng trong môn Toán lớp 7 nhé.
Tam giác đều, tam giác cân, tam giác vuông là mọi giả thiết về hình học tập trở đề nghị rất không còn xa lạ với họ trong môn Toán mà ai cũng cần yêu cầu biết. Bài viết dưới đây của công ty chúng tôi muốn trình làng đến các bạn những Tích Chất và Cách Tính Đường Cao Tam Giác Đều, Vuông, cân nặng và các đặc tính riêng của chúng nhé!
1. Một vài tính hóa học về đường cao trong tam giác
Trước tiên chúng hiểu mặt đường cao trong tam giác chính là đoạn thẳng vuông góc bắt đầu từ đỉnh của tam giác cho cạnh đáy đối diện của tam giác đó. Từng một tam giác sẽ có 3 con đường cao và khoảng cách giữa đỉnh cùng cạnh lòng là độ dài mặt đường cao. Cùng mày mò với shop chúng tôi một số tính chất trong những loại tam giác đặc biệt sau đây.
1.1 đặc thù ba con đường cao vào tam giác thường
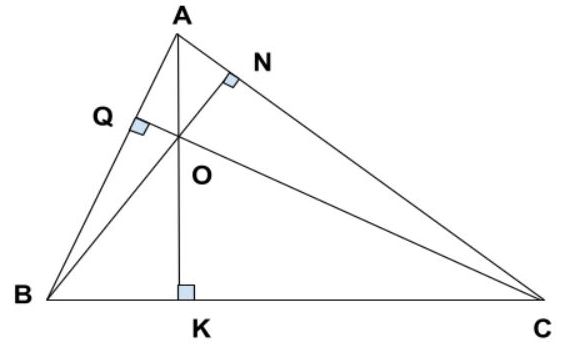
Cùng với giả thiết đề việc và tác dụng đã được những nhà toán học trên toàn quả đât đã chứng minh có sẵn. Hiện nay, họ đã vượt nhận các tích hóa học của con đường cao trong tam giác hay như sau. Ba đường cao của một tam giác đã giao nhau tại một điểm. Cùng giao điểm của bố đường cao sẽ được coi là trực vai trung phong của tam giác đó.
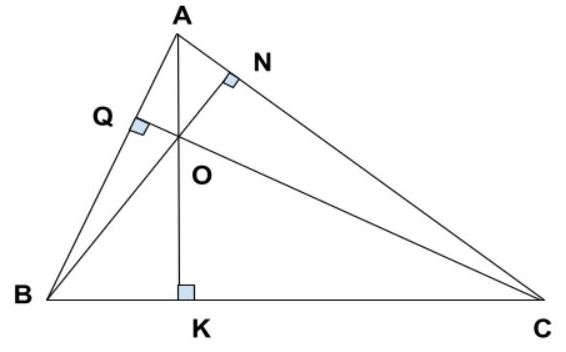
Tính chất ba đường cao vào tam giác thường
1.2 đặc thù đường cao trong tam giác vuông
Đối với tam giác vuông, đấy là tam giác đặc trưng so với tam giác thường bởi nó có một góc vuông. Chủ yếu điều này để cho đường cao tam giác vuông đang có một vài tính chất khác hoàn toàn như sau đây. Những tính chất này bọn họ cần bắt buộc ghi nhớ nhằm để rất có thể giúp ích trong quy trình làm bài tập và áp dụng trong cuộc sống thường ngày nhé:
Tính chất thứ 1: vào tam giác vuông, tích của mặt đường cao với cạnh huyền khớp ứng chính bởi tích của nhị cạnh góc vuông trong tam giácTính chất thứ 2: vào tam giác vuông ta có bình phương của cạnh góc vuông bởi cạnh huyền nhân mặt đường cao tương xứng chiếu bên trên cạnh huyền đóTính hóa học thứ 3: trong tam giác vuông, bình phương của đường cao trên cạnh huyền chính bằng tích của hai hình chiếu trên cạnh huyền của nhị cạnh góc vuông Tính hóa học thứ 4: vào tam giác vuông, nghịch đảo của bình phương từng cạnh góc vuông bằng nghịch hòn đảo của bình phương con đường cao1.3 đặc thù đường cao vào tam giác cân
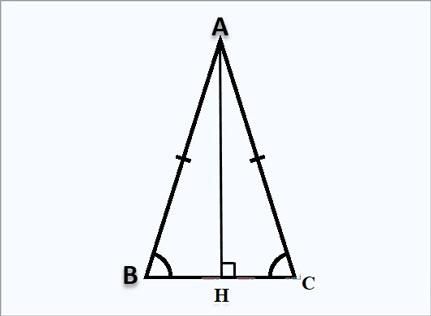
Đường cao vào tam giác cân
Tam giác cân đó là tam giác gồm tính chất nhất là có độ dài hai kề bên bằng nhau cùng 2 góc ở lòng cũng bởi nhau. Chính vì vậy, Đường cao vào tam giác cân đang có một trong những tính chất đặc trưng mà các bạn học cần phải biết như sau:
Đầu tiên, mặt đường cao vào tam giác đó là đoạn trực tiếp vuông góc bắt đầu từ đỉnh đến cạnh đáy. Và con đường cao vào tam giác cân sẽ giúp đỡ chia tam giác cân nặng này thành 2 tam giác cân đối nhau khác.Thứ hai, mặt đường cao khởi đầu từ đỉnh ứng cùng với cạnh đáy tất cả chân đường cao là trung điểm của cạnh đáy. Vì vậy nó đồng thời là mặt đường cao, đường phân giác cùng cũng là mặt đường trung trực của tam giác cân.Bạn đang xem: Tính chiều cao tam giác
Bên cạnh đó, trong tam giác vuông cân nặng là ngôi trường hợp đặc trưng của tam giác cân và tam giác vuông. Chính vậy mà, đường cao tam giác vuông cân sẽ có những tính chất giống như như trong tam giác cân nặng và tam giác vuông. Và con đường cao trong tam giác vuông cân sẽ chia tam giác thành nhị tam giác vuông cân.
1.4 Đường cao vào tam giác đều phải có tính hóa học gì?
Tam giác gần như là tam giác thường đáp ứng đầy đủ các đk là tất cả 3 cạnh bằng nhau. Đồng thời 3 góc bao gồm trong tam giác đều bởi và bằng 60 độ cần độ dài của 3 đường cao tam giác đều bằng nhau. Lân cận đó, con đường cao của tam giác đều sở hữu một số tính chất đặc trưng nổi nhảy mà bạn nên tìm hiểu như sau:
Thứ nhất, một tam giác đều có tới 3 mặt đường cao. Và đa số đường cao khớp ứng đều phát xuất từ các định cùng kẻ vuông góc xuống các cạnh đáy còn lại tương ứng vào tam giác.Thứ hai, 3 con đường cao trong tam giác số đông sẽ phân tách đôi những góc làm việc đỉnh thành 2 góc đều bằng nhau và đều bằng 30oThứ ba, mặt đường cao trong tam giác đều không chỉ đồng thời là con đường trung trực, mặt đường phân giác mà còn là một đường trung tuyến đường trong tam giác. Vì trong tam giác đều sẽ có các cạnh đều nhau và những góc bởi nhau.Thứ tư, đường cao đi qua trung điểm của cạnh lòng và chia cạnh đáy thành 2 phần bằng nhau.Thứ năm, mỗi mặt đường cao vào tam giác các sẽ phân tách tam giác thành 2 tam giác cân nhau có diện tích giống hệt giống tam giác cân và tam giác vuông.Xem thêm: Những Câu Slogan Hay Về Kinh Doanh Các Công Ty, Thương Hiệu Lớn 2021
2. Những công thức tính độ dài mặt đường cao vào tam giác
Hiện nay, những công thức tính độ dài mặt đường cao đầy đủ đã được phát hiện nay và chứng minh do đông đảo nhà toán học thời trước. Vì thế mà trong quá trình giải bài tập, núm vì bọn họ phải minh chứng các phương pháp lại từ đầu để search ra công thức thì bạn cũng có thể ghi nhớ và áp dụng một số trong những công thức sau đây để đưa ra đáp án nhanh và đúng chuẩn hơn nhé!
2.1 mày mò công thức tính con đường cao trong tam giác không sệt biệt
Chúng ta hoàn toàn có thể nhận thấy rất đơn giản dễ dàng tam giác thường có 3 cạnh khác nhau, tạm call chúng là a, b, c, suy ra nửa chu vi phường = (a + b + c)/2. Từ kia ta bao gồm công thức tính độ cao trong tam giác thường như sau: h= 2. P. P-ap-b(p-c)a
2.2 cách tính đường cao trong tam giác gần như nhanh gọn
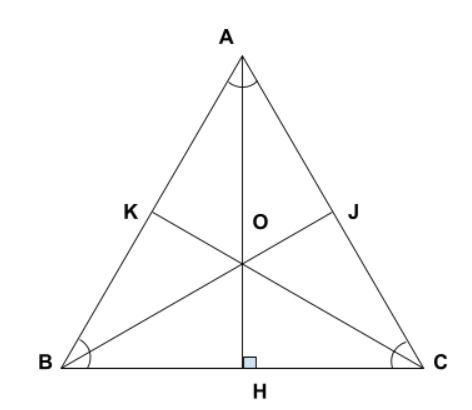
Tính đường cao tam giác phần lớn và hình vẽ đường cao trong tam giác đều
Tam giác phần đa là tam giác có cha cạnh đều nhau và tía góc bằng nhau, bao gồm vậy mà đối với đường cao vào tam giác đa số thì đặc điểm cố hữu của mặt đường cao đó là 3 mặt đường cao trong tam giác đều phải sở hữu độ dài bởi nhau. Và bao gồm đầy vừa đủ các đặc thù giống nhau.
Do đó, mang sử cạnh của tam giác đều phải sở hữu độ lâu năm là x thì đường cao trong tam giác phần đa sẽ có thể được tính theo bí quyết đã chứng tỏ như sau: H = x. 32.
2.3 một số cách tính con đường cao vào tam giác vuông
Dựa vào những tính chất đã chứng minh của đường cao vào tam giác vuông thì đường cao vào tam giác vuông ta đúc rút được một số trong những cách tính độ dài con đường cao trong tam giác vuông nhưng bạn cần phải biết như sau:
X. H = Y.Z (theo đó X,Y,Z theo thứ tự là các cạnh của tam giác vuông, X là cạnh huyền)H2 = Y’. Z’ (Y’, Z’ lần lượt là hình chiếu của những cạnh góc vuông bên trên cạnh huyền)1H2 = 1Y2 + 1Z22.4 Công thức, cách tính đường cao trong tam giác cân đơn giản nhất
Đối cùng với tam giác cân nặng là tam giác gồm hai ở kề bên bằng nhau và hai góc bên bằng nhau. Chính vì vậy mà mặt đường cao trong tam giác cân bao hàm tính chất khác biệt với tam giác thường. Vì vậy, phương pháp tính đường cao của tam giác cân nặng có phương pháp tính khác nhau cụ thể như sau:
Giả sử tam giác cân tất cả 2 cạnh bên có độ dài bởi a, cạnh đáy bằng b. Trường đoản cú đó phụ thuộc vào tính chất trung điểm cũng tương tự định lí Pi- ta-go chúng ta có công thức tính đường cao tam giác cân như sau:
H = 4a2- b24
Như vậy, bài viết trên đã khiến cho bạn có thêm phần lớn kiến thức hữu ích về phần đông Tính Chất và Cách Tính Đường Cao Tam Giác Đều, Vuông, cân ở lớp 7. Cùng tiếp theo họ sẽ có tác dụng quen với những tính chất của tam giác đồng dạng lớp 8. Hãy thường xuyên theo dõi chúng tôi để hiểu biết thêm những thông tin khác về toán học nhé.














