Câu hỏi:
04/12/2022 54,356
Chọn B.
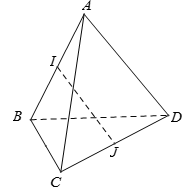
Xét tam giác ICD có J là trung điểm đoạn CD .
Ta có:
Vì tam giác ABC có AB = AC và
Nên tam giác ABC đều. Suy ra:
Tương tự động tao sở hữu tam giác ABD đều nên
Xét
Nhà sách VIETJACK:
🔥 Đề ganh đua HOT:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD có toàn bộ những cạnh đều vì chưng a . Gọi I và J lần lượt là trung điểm của SC và BC . Số đo của góc (IJ, CD) bằng
Câu 2:
Cho nhị vectơ thỏa mãn: . Độ nhiều năm vectơ bằng?
Câu 3:
Cho tứ diện ABCD có AB = AC = AD và . Hãy xác lập góc thân thích cặp vectơ và ?
Câu 4:
Cho nhị vectơ thỏa mãn: . Xét nhị vectơ . Gọi α là góc thân thích nhị vectơ . Chọn xác minh đích thị.
Câu 5:
Cho tứ diện ABCD . Gọi M, N lần lượt là trung điểm những cạnh BC và AD . Cho biết AB = CD = 2a và . Tính góc thân thích hai tuyến đường trực tiếp AB và CD .
Câu 6:
Cho hình chóp S.ABC có SA = SB = SC và . Hãy xác lập góc thân thích cặp vectơ và ?
