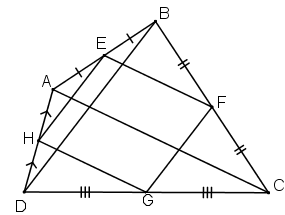
Ta có: EB = EA, FB = FC (gt)
⇒ EF là đàng khoảng của ΔABC
⇒ EF // AC và EF = AC/2.
HA = HD, HC = GD
⇒ HG là đàng khoảng của ΔADC
⇒ HG // AC và HG = AC/2.
Do cơ EF // HG, EF = HG
⇒ EFGH là hình bình hành.
a) Hình bình hành EFGH là hình chữ nhật ⇔ EH ⊥ EF
⇔ AC ⊥ BD (vì EH // BD, EF// AC)
b) Hình bình hành EFGH là hình thoi
⇔ EF = EH
⇔ AC = BD (Vì EF = AC/2, EH = BD/2)
c) EFGH là hình vuông
⇔ EFGH là hình thoi và EFGH là hình chữ nhật
⇔ AC = BD và AC ⊥ DB.
Câu 1:
Cho tam giác ABC vuông bên trên A, đàng trung tuyến AM. Gọi D là trung điểm của AB, E là vấn đề bịp bợm xứng với M qua quýt D.
a) Chứng minh rằng điểm E đối xứng với điểm M qua quýt AB.
b) Các tứ giác AEMC, AEBM là hình gì? Vì sao?
c) Cho BC = 4cm, tính chu vì thế tứ giác AEBM.
d) Tam giác vuông ABC sở hữu ĐK gì thì AEBM là hình vuông?