Câu hỏi:
12/07/2024 24,636
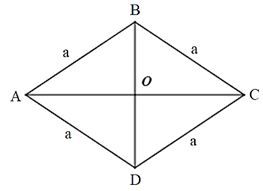
Ta có:
Nhà sách VIETJACK:
🔥 Đề đua HOT:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho và a, b là những góc nhọn. Tính A = sin(a – b).
Câu 2:
Cho hình chóp S.ABCD với ABCD sở hữu những cạnh đối lập ko tuy nhiên song cùng nhau và M là 1 trong điểm bên trên SA. Tìm uỷ thác điểm của đường thẳng liền mạch và MC và (SBD).
Câu 3:
Cho hình chóp S.ABCD sở hữu lòng ABCD là hình bình hành. Gọi M là trung điểm của SC.
a) Tìm uỷ thác điểm I của AM và (SBD).
b) Tìm uỷ thác điểm P.. của SD và (ABM). Chứng minh rằng P.. là trung điểm của SD.
c) Gọi N là vấn đề tùy ý bên trên cạnh AB. Tìm uỷ thác điểm K của MN và (SBD).
Cho hình chóp S.ABCD sở hữu lòng ABCD là hình bình hành. Gọi M là trung điểm của SC.
a) Tìm uỷ thác điểm I của AM và (SBD).
b) Tìm uỷ thác điểm P.. của SD và (ABM). Chứng minh rằng P.. là trung điểm của SD.
c) Gọi N là vấn đề tùy ý bên trên cạnh AB. Tìm uỷ thác điểm K của MN và (SBD).
Câu 4:
Cho hình thang MNPQ (MN // PQ), sở hữu MP = NQ. Qua N kẻ đàng thắng song
song với MP, rời đường thẳng liền mạch PQ bên trên K. Chứng minh:
a) MNPQ là hình thang cân nặng.
b) ∆MPQ = ∆NQP.
c) Tam giác NKQ cân nặng.
Cho hình thang MNPQ (MN // PQ), sở hữu MP = NQ. Qua N kẻ đàng thắng song
song với MP, rời đường thẳng liền mạch PQ bên trên K. Chứng minh:
a) MNPQ là hình thang cân nặng.
b) ∆MPQ = ∆NQP.
c) Tam giác NKQ cân nặng.
Câu 5:
Cho hình vỏ hộp chữ nhật ABCD.A'B'C'D' sở hữu AB = 1, BC = 2, AA' = 2. Khoảng cơ hội thân ái hai tuyến đường trực tiếp AD' và DC' bằng? (tham khảo hình)
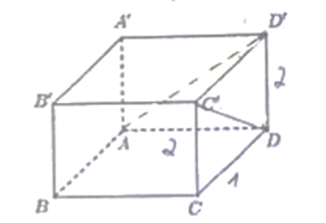
Cho hình vỏ hộp chữ nhật ABCD.A'B'C'D' sở hữu AB = 1, BC = 2, AA' = 2. Khoảng cơ hội thân ái hai tuyến đường trực tiếp AD' và DC' bằng? (tham khảo hình)

Câu 6:
Cho khối chóp S.ABCD sở hữu lòng ABCD là hình bình hành, SA = SB = SC = AC = a, SB tạo ra với mặt mày bằng phẳng (SAC) một góc 30°. Tính thể tích khối chóp.
