Lời giải của Tự Học 365
Giải chi tiết:
Xét hệ xa lánh bao gồm nhì phần của thương hiệu lửa trước và sau thời điểm tách.
Ta có:
\(\left\{ \begin{gathered}
{m_1} = 400kg \hfill \\
{m_2} = 200kg \hfill \\
\end{gathered} \right.\)
(m2 là phần bị tách)
Gọi \(\overrightarrow{v}\) là véc tơ vận tốc tức thời của thương hiệu lửa trước lúc tách.
\(\overrightarrow{{{v}_{1}}};\overrightarrow{{{v}_{2}}}\) theo lần lượt là véc tơ vận tốc tức thời của m1, m2 sau thời điểm tách.
Động lượng của hệ khi trước lúc tách :
\(\overrightarrow{{{p}_{tr}}}=\left( {{m}_{1}}+{{m}_{2}} \right).\overrightarrow{v}=600.\overrightarrow{v}\)
Động lượng của hệ khi sau thời điểm tách :
\(\overrightarrow{{{p}_{s}}}={{m}_{1}}.\overrightarrow{{{v}_{1}}}+{{m}_{2}}.\overrightarrow{{{v}_{2}}}=400.\overrightarrow{{{v}_{1}}}+200.\overrightarrow{{{v}_{2}}}\)
Động lượng được bảo toàn nên :
\(600.\overrightarrow{v}=400.\overrightarrow{{{v}_{1}}}+200.\overrightarrow{{{v}_{2}}}\,\,\,\left( * \right)\)
Với \(\overrightarrow{{{v}_{2}}}\) là véc tơ vận tốc tức thời của phần tách tách đối với khu đất.
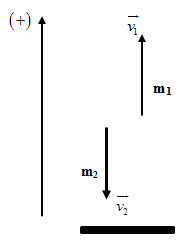
Ta sở hữu : \(\overrightarrow{{{v}_{2}}}=\overrightarrow{{{v}_{21}}}+\overrightarrow{{{v}_{1}}}\)
Do : \(\overrightarrow{{{v}_{21}}}\,\uparrow \downarrow \overrightarrow{{{v}_{1}}}\,\Rightarrow {{v}_{2}}={{v}_{21}}-{{v}_{1}}=150-{{v}_{1}}\)
Chọn chiều dương phía lên. Chiếu (*) lên chiều dương tao được :
\(\begin{gathered}
600v = 400.{v_1} - 200{v_2} \Leftrightarrow 600.200 = 400.{v_1} - 200\left( {150 - {v_1}} \right) \hfill \\
\Leftrightarrow 120000 = 400.{v_1} - 30000 + 200.{v_1} \hfill \\
\Leftrightarrow 600{v_1} = 150000 \Rightarrow {v_1} = 250m/s \hfill \\
\end{gathered} \)
Chọn C.
