Đề kiểm tra học kì 2 Toán 10 - Đề số 4 - Cánh diều | Đề thi, đề kiểm tra Toán lớp 10

Đề bài

Trắc nghiệm ( 7 điểm)

Câu 1. Lớp \(10\;A\) với 21 chúng ta phái nam và 18 cô gái. Hỏi với từng nào cơ hội lựa chọn một học viên thực hiện lớp trưởng?

A. 168 cơ hội. B. 29 cơ hội. C. 39 cơ hội. D. 158 cơ hội.

Câu 2. Một quán ăn đáp ứng 5 quà ăn vặt và 2 loại đồ uống. Hỏi chúng ta Mai với từng nào phương pháp để gọi một thức ăn và một loại nước uống?

A. 5 cơ hội. B. 7 cơ hội. C. 10 cơ hội. D. 3 cơ hội.

Câu 3. Ví dụ nào là sau đó là một ví dụ về hoán vị?

A. Số cơ hội xếp sản phẩm bám theo sản phẩm dọc của 10 chúng ta.

B. Số cơ hội phân chia 10 chúng ta nhập nhì group.

C. Số cơ hội lựa chọn ra 4 chúng ta nhập group 10 chúng ta.

D. Số cơ hội xếp sản phẩm của 5 chúng ta nhập group 10 chúng ta.

Câu 4. Đội tuyển chọn toán với 5 chúng ta phái nam và 7 cô gái. Giáo viên nên lựa chọn ra một group tư chúng ta. Hỏi nghề giáo với từng nào cơ hội chọn?

A. \(\frac{{12!}}{{4!}}\). B. 12!. C. \(C_{12}^4\). D. \(A_{12}^4\).

Câu 5. Cho tụ tập \(A = \{ 1;2;3;4;5;6;7\} \). Hỏi với từng nào cơ hội lập được số với phụ thân chữ số không giống nhau kể từ những chữ số nằm trong tụ tập \(A\)?

A. \(C_7^3\). B. \(C_7^4\). C. \(A_7^3\). D. \(A_7^4\).

Câu 6. Số cơ hội phân chia 10 học viên trở thành phụ thân group theo lần lượt với \(2,3,5\) học viên là:

A. \(C_{10}^2 + C_{10}^3 + C_{10}^5\).

B. \(C_{10}^2 \cdot C_8^3 \cdot C_5^5\).

C. \(C_{10}^2 + C_8^3 + C_5^5\).

D. \(C_{10}^5 + C_5^3 + C_2^2\).

Câu 7. Có từng nào cơ hội xếp 5 sách Văn không giống nhau và 7 sách Toán không giống nhau bên trên một kệ sách nhiều năm nếu như những sách Văn nên xếp kề nhau?

A. 5!.7!. B. \(2.5!.7!\). C. \(5!.8!\). D. \(12!\).

Câu 8. Giả sử tớ sử dụng 5 màu sắc nhằm tô cho tới 3 nước không giống nhau bên trên phiên bản trang bị và không tồn tại màu sắc nào là được sử dụng nhì phen. Số những phương pháp để lựa chọn những màu sắc nhớ dùng là:

A. \(\frac{{5!}}{{2!}}\).

B. 8.

C. \(\frac{{5!}}{{3!2!}}\).

D. \({5^3}\).

Câu 9. Khai triển của \({(x + 1)^4}\) là:

A. \({x^4} + 2{x^2} + 1\).

B. \({x^4} + 4{x^3} + 6{x^2} + 4x + 1\).

C. \({x^4} + 5{x^3} + 10{x^2} + 5x + 1\).

D. \({x^4} + 3{x^3} + 4{x^2} + 3x + 1\).

Câu 10. Hệ số của \({x^3}\) nhập khai triển của \({(2x + 1)^4}\) là:

A. 4. B. 6. C. 10. D. 32.

Câu 11. Giả sử với khai triển \({(1 - 2x)^n} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_n}{x^n}\). Tìm \({a_4}\) biết \({a_0} + {a_1} + {a_2} = 31\).

A. 80. B. \( - 80\). C. 40. D. \( - 40\).

Câu 12. Hình chữ nhật với những cạnh:\(x = 2m \pm 1cm\), \(y = 5m \pm 2cm\). Diện tích hình chữ nhật và sai số vô cùng của độ quý hiếm cơ là:

A. \(10{m^2}\) và \(900c{m^2}\).

B. \(10{m^2}\) và \(500c{m^2}\).

C. \(10{m^2}\) và \(400c{m^2}\).

D. \(10{m^2}\) và \(1404\;c{m^2}\).

Câu 13. Một hình chữ nhật với diện tích S là \(S = 108,57c{m^2} \pm 0,06c{m^2}.\) Số những chữ số có thể của \(S\)là:

A. \(5.\) B. \(4.\) C. \(3.\) D. \(2.\)

Câu 14. Cho tam giác \(ABC\) có tính nhiều năm phụ thân cạnh đo được như sau \(a = 12\,{\rm{cm}} \pm 0,2\,{\rm{cm}}\); \(b = 10,2\,{\rm{cm}} \pm 0,2\,{\rm{cm}}\); \(c = 8\,{\rm{cm}} \pm 0,1\,{\rm{cm}}\). Tính chu vi \(P\) của tam giác và Đánh Giá sai số vô cùng, sai số kha khá của số sấp xỉ của chu vi qua loa quy tắc đo.

A. \(1,6\% \) B. \(1,7\% \) C. \(1,662\% \) D. \(1,66\% \)

Câu 15. Số áo bán tốt nhập một quý ở cửa hàng buôn bán áo sơ-mi phái nam được tổng hợp như sau:

Cỡ áo

Tần số

(Số áo buôn bán được)

126

125

110

Giá trị kiểu mốt của bảng phân bổ tần số bên trên bằng

A. \(38\). B. \(126\). C. \(42\). D. \(12\).

Câu 16. Tiền bổng mỗi tháng của \(7\) nhân viên cấp dưới nhập một doanh nghiệp lớn du ngoạn theo lần lượt là:\(6,5\); \(8,4\); \(6,9\); \(7,2\); \(2,5\); \(6,7\); \(3,0\) (đơn vị: triệu đồng). Số trung vị của sản phẩm số liệu tổng hợp bên trên bằng

A. \(6,7\) triệu đồng.

B. \(7,2\) triệu đồng.

C. \(6,8\) triệu đồng.

D. \(6,9\) triệu đồng.

Câu 17. Cho phương sai của những số liệu bởi vì \(4\). Tìm phỏng chếch chuẩn chỉnh.

A. \(4\). B. \(2\). C. \(16\). D. \(8\).

Câu 18. Độ chếch chuẩn chỉnh là

A. Căn bậc nhì của phương sai.

B. Bình phương của phương sai.

C. Một nửa của phương sai.

D. Không nên những công thức bên trên.

Câu 19. Có 100 học viên tham gia kì thi đua học viên xuất sắc Toán (thang điểm 20). Kết trái ngược cho tới nhập bảng sau:

Khi cơ phỏng chếch chuẩn chỉnh là

A. \(1,98\). B. \(3,96\). C. \(15,23\) D. \(1,99\).

Câu trăng tròn. Điểm thi đua của lớp 10C của một ngôi trường Trung học tập Phổ Thông được trình diễn trên bảng phân bổ tần số sau:

Phương sai của bảng phân bổ tần số tiếp tục cho tới là:

A. \(0,94\) B. \(3,94.\) C. \(2,94.\) D. \(1,94.\)

Câu 21. Điểm thi đua môn Toán lớp 10A₂ của một Trường trung học tập phổ thông được trình diễn trên bảng phân bổ tần số sau

Điểm thi	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)
Tần số	\(7\)	\(5\)	\(10\)	\(12\)	\(4\)	\(2\)	\(n = 40\)

Trong những độ quý hiếm sau đây, độ quý hiếm nào là sớm nhất với phương sai của bảng phân bổ tần số trên?

A. \(0,94\). B. \(3,94\). C. \(2,94\). D. \(1,94\).

Câu 22. Gieo một đồng xu phẳng phiu và đồng hóa học liên tục phụ thân phen. Gọi \(A\) là đổi thay cố “Có tối thiểu nhì mặt mũi sấp xuất hiện nay liên tiếp” và \(B\) là đổi thay cố “Kết trái ngược phụ thân phen gieo là như nhau”. Xác quyết định đổi thay cố \(A \cup B.\)

A. \(A \cup B = \left\{ {SSS,\,SSN,\,NSS,\,SNS,\,NNN} \right\}\)

B. \(A \cup B = \left\{ {SSS,\,NNN} \right\}\).

C. \(A \cup B = \left\{ {SSS,\,SSN,\,NSS,\,NNN} \right\}\)

D. \(A \cup B = \Omega \).

Câu 23. Gieo tình cờ một đồng xu tiền phẳng phiu và đồng hóa học \(5\) phen. Tính số thành phần không khí kiểu.

A. \(64\). B. \(10\). C. \(32\). D. \(16\).

Câu 24. Gieo một con cái súc sắc. Xác suất nhằm mặt mũi \(6\) chấm xuất hiện nay.

A. \(\frac{1}{6}\). B. \(\frac{5}{6}\). C. \(\frac{1}{2}\). D. \(\frac{1}{3}\).

Câu 25. Gieo một con cái súc sắc phẳng phiu và đồng hóa học gấp đôi. Tính phần trăm nhằm tổng số chấm nhập nhì phen gieo nhỏ rộng lớn 6.

A. \(\frac{2}{9}\).

B. \(\frac{{11}}{{36}}\).

C. \(\frac{1}{6}\).

D. \(\frac{5}{{18}}\).

Câu 26. Trong hệ trục \(Oxy,\) cho tới Elip \(\left( E \right)\) với những xài điểm \({F_1}\left( { - 4;0} \right),{F_2}\left( {4;0} \right)\) và một điểm \(M\) phía trên \(\left( E \right)\). hiểu rằng chu vi của tam giác \(M{F_1}{F_2}\) bởi vì 18. Xác quyết định tâm sai e của \(\left( E \right).\)

A. \(e = \frac{4}{5}\).

B. \(e = \frac{4}{{18}}\).

C. \(e = - \frac{4}{5}\).

D. \(e = \frac{4}{9}\).

Câu 27. Trong mặt mũi bằng phẳng toạ phỏng \(Oxy\), cho tới \(\vec a = (1;2),\vec b = (3; - 3)\). Toạ phỏng của vectơ \(\vec c = 3\vec a - 2\vec b\) là:

A. \(( - 3;12)\).

B. \((3;12)\).

C. \((9;0)\).

D. \(( - 3;0)\).

Câu 28. Trong mặt mũi bằng phẳng toạ phỏng \(Oxy\), cho tới phụ thân điểm \(A( - 1;2),B(2; - 2),C(3;1)\). Toạ phỏng của vectơ \(\overrightarrow {AB} + \overrightarrow {BC} \) là:

A. \(( - 4; - 1)\). B. \((4; - 1)\). C. \(( - 4;1)\). D. \((4;1)\).

Câu 29. Một đường thẳng liền mạch với từng nào vectơ pháp tuyến?

A. 0. B. 1. C. 2. D. Vô số.

Câu 30. Phương trình tổng quát lác của đường thẳng liền mạch \(\Delta \) trải qua điểm \(M\left( {{x_0};{y_0}} \right)\) và với vectơ pháp tuyến \(\vec n(a;b)\) là:

A. \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}\).

B. \(b\left( {x - {x_0}} \right) - a\left( {y - {y_0}} \right) = 0\).

C. \(a\left( {x + {x_0}} \right) + b\left( {y + {y_0}} \right) = 0\).

D. \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).

Câu 31. Đường Hyperbol \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\) với cùng 1 xài điểm là vấn đề nào là sau đây ?

A.\(\left( { - 5;0} \right)\).

B.\(\left( {0;\sqrt 7 } \right)\).

C. \(\left( {\sqrt 7 ;0} \right)\).

D. \(\left( {0;5} \right)\).

Câu 32. Đường elip \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{7} = 1\) với xài cự bằng

A. \(3\). B. \(9\). C. \(6\). D. \(18\).

Câu 33. Trong mặt mũi bằng phẳng \(Oxy\), phương trình nào là sau đó là phương trình của lối tròn?

A. \({x^2} + 2{y^2} - 4x - 8y + 1 = 0\).

B. \({x^2} + {y^2} - 4x + 6y - 12 = 0\).

C. \({x^2} + {y^2} - 2x - 8y + trăng tròn = 0\).

D. \(4{x^2} + {y^2} - 10x - 6y - 2 = 0\).

Câu 34. Trong mặt mũi bằng phẳng \(Oxy\), lối tròn xoe \(\left( C \right):{x^2} + {y^2} + 4x + 6y - 12 = 0\) với tâm là.

A. \(I\left( { - 2; - 3} \right)\). B. \(I\left( {2;3} \right)\). C. \(I\left( {4;6} \right)\). D. \(I\left( { - 4; - 6} \right)\).

Câu 35. Đường tròn xoe \(\left( C \right)\) trải qua nhì điểm \(A\left( {1;1} \right)\), \(B\left( {5;3} \right)\) và với tâm \(I\) nằm trong trục hoành với phương trình là

A. \({\left( {x + 4} \right)^2} + {y^2} = 10\).

B. \({\left( {x - 4} \right)^2} + {y^2} = 10\).

C. \({\left( {x - 4} \right)^2} + {y^2} = \sqrt {10} \).

D. \({\left( {x + 4} \right)^2} + {y^2} = \sqrt {10} \).

Tự luận (3 điểm)

Câu 1. Từ một group 30 học viên lớp 12 bao gồm 15 học viên khối \(A,10\) học viên khối \(B\) và 5 học viên khối \(C\), cần thiết lựa chọn ra 15 học viên, chất vấn với từng nào cơ hội lựa chọn sao cho:

a) Số học viên từng khối là bởi vì nhau?

b) Có tối thiểu 5 học viên khối \(A\) và với chính 2 học viên khối \(C\)?

Câu 2. Cho biểu thức \(Q = {(xy - 1)^5}\).

a) Viết khai triển biểu thức \(Q\) bởi vì nhị thức Newton.

b) Tìm số hạng với chứa chấp \({x^2}{y^2}\) nhập khai triển bên trên.

Câu 3. Người tớ tổ chức phỏng vấn một vài người về quality của một loại thành phầm mới nhất. người khảo sát đòi hỏi cho tới điểm thành phầm ( thang điểm 100) thành quả như sau:

80 65 51 48 45 61 30 35 84 83 60 58 75

72 68 39 41 54 61 72 75 72 61 58 65

a) Tìm phương sai và phỏng chếch chuẩn chỉnh. Nhận xét gì về những thành quả sẽ có được.

b) Tìm khoảng tầm đổi thay thiên, khoảng tầm tứ phân vị

c) Tìm độ quý hiếm bất thường

Câu 4. Cho tam giác \(ABC\) với \(A( - 1; - 2)\) và phương trình đường thẳng liền mạch chứa chấp cạnh \(BC\) là \(x - nó + 4 = 0\).

a) Viết phương trình lối cao \(AH\) của tam giác.

b) Viết phương trình lối khoảng ứng với cạnh lòng \(BC\) của tam giác.

Lời giải

HƯỚNG DẪN GIẢI CHI TIẾT

THỰC HIỆN: BAN CHYÊN MÔN LOIGIAIHAY.COM

I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).

Câu 1. Lớp \(10\;A\) với 21 chúng ta phái nam và 18 cô gái. Hỏi với từng nào cơ hội lựa chọn một học viên thực hiện lớp trưởng?

A. 168 cơ hội. B. 29 cơ hội. C. 39 cơ hội. D. 158 cơ hội.

Phương pháp

Áp dụng quy tắc cộng

Lời giải

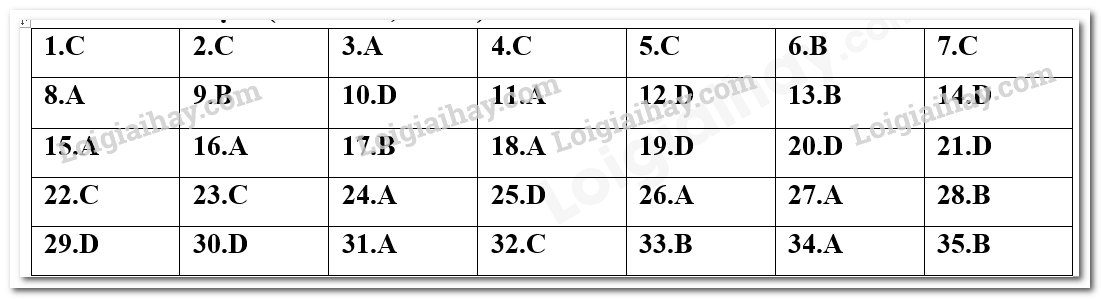
Chọn C.

Áp dụng quy tắc nằm trong số cơ hội lựa chọn một học viên thực hiện lớp trưởng là \(21 + 18 = 39\)

Câu 2. Một quán ăn đáp ứng 5 quà ăn vặt và 2 loại đồ uống. Hỏi chúng ta Mai với từng nào phương pháp để gọi một thức ăn và một loại nước uống?

A. 5 cơ hội. B. 7 cơ hội. C. 10 cơ hội. D. 3 cơ hội.

Phương pháp

Áp dụng quy tắc nhân

Lời giải

Chọn C.

Áp dụng quy tắc nhân số phương pháp để gọi một thức ăn và một loại đồ uống là \(21 + 18 = 39\)

Câu 3. Ví dụ nào là sau đó là một ví dụ về hoán vị?

A. Số cơ hội xếp sản phẩm bám theo sản phẩm dọc của 10 chúng ta.

B. Số cơ hội phân chia 10 chúng ta nhập nhì group.

C. Số cơ hội lựa chọn ra 4 chúng ta nhập group 10 chúng ta.

D. Số cơ hội xếp sản phẩm của 5 chúng ta nhập group 10 chúng ta.

Phương pháp

Áp dụng công thức hoán vị

Lời giải

Chọn A.

Câu 4. Đội tuyển chọn toán với 5 chúng ta phái nam và 7 cô gái. Giáo viên nên lựa chọn ra một group tư chúng ta. Hỏi nghề giáo với từng nào cơ hội chọn?

A. \(\frac{{12!}}{{4!}}\). B. 12!. C. \(C_{12}^4\). D. \(A_{12}^4\).

Phương pháp

Áp dụng công thức tổ hợp

Lời giải

Chọn C.

Số học viên ở team tuyển chọn toán là \(5 + 7 = 12\)

Vậy nghề giáo với \(C_{12}^4\) cơ hội lựa chọn.

A. \(C_7^3\). B. \(C_7^4\). C. \(A_7^3\). D. \(A_7^4\).

Phương pháp

Áp dụng công thức chỉnh hợp

Lời giải

Chọn C.

Số cơ hội lập được số với phụ thân chữ số không giống nhau kể từ những chữ số nằm trong tập luyện hợp là \(A_7^3\)

Câu 6. Số cơ hội phân chia 10 học viên trở thành phụ thân group theo lần lượt với \(2,3,5\) học viên là:

A. \(C_{10}^2 + C_{10}^3 + C_{10}^5\). B. \(C_{10}^2 \cdot C_8^3 \cdot C_5^5\).

C. \(C_{10}^2 + C_8^3 + C_5^5\). D. \(C_{10}^5 + C_5^3 + C_2^2\).

Phương pháp

Áp dụng công thức tổ hợp

Lời giải

Chọn \(B\).

Chọn 2 nhập 10 học viên nhập group loại nhất: với \(C_{10}^2\) cơ hội.

Chọn 3 nhập 8 học viên sót lại nhập group loại hai: với \(C_8^3\) cơ hội.

Chọn 5 nhập 5 học viên sau cuối nhập group loại ba: với \(C_5^5\) cơ hội.

Vậy với \(C_{10}^2 \cdot C_8^3 \cdot C_5^5\) cơ hội lựa chọn vừa lòng đề bài bác.

A. 5!.7!.

B. \(2.5!.7!\).

C. \(5!.8!\).

D. \(12!\).

Phương pháp

Áp dụng công thức hoán vị

Lời giải

Chọn C

Sắp xếp 5 quyển Văn cộng đồng một group ngang (nhóm \(V)\): với 5! cơ hội.

Sắp xếp 7 quyển Toán với \(V\) (ta coi như bố trí 8 phần tử): với \(8!\) cơ hội. Vậy với toàn bộ \(5!.8!\) cơ hội bố trí vừa lòng đề bài bác.

A. \(\frac{{5!}}{{2!}}\). B. 8. C. \(\frac{{5!}}{{3!2!}}\). D. \({5^3}\).

Phương pháp

Áp dụng công thức chỉnh hợp

Lời giải

Chọn A

Chọn 3 nhập 5 màu sắc nhằm tô nhập 3 nước không giống nhau: với \(A_5^3 = \frac{{5!}}{{2!}}\) cơ hội.

Câu 9. Khai triển của \({(x + 1)^4}\) là:

A. \({x^4} + 2{x^2} + 1\).

B. \({x^4} + 4{x^3} + 6{x^2} + 4x + 1\).

C. \({x^4} + 5{x^3} + 10{x^2} + 5x + 1\).

D. \({x^4} + 3{x^3} + 4{x^2} + 3x + 1\).

Phương pháp

Áp dụng công thức \({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)

Lời giải

Chọn B

Áp dụng công thức \({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)

Câu 10. Hệ số của \({x^3}\) nhập khai triển của \({(2x + 1)^4}\) là:

A. 4. B. 6. C. 10. D. 32.

Phương pháp

Áp dụng công thức \({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)

Lời giải

Chọn D

Số hạng chúa \({x^3}\) nhập khai triển của \({(2x + 1)^4}\) là \(C_4^1{(2x)^3}.1\)

Hệ số của \({x^3}\) nhập khai triển của \({(2x + 1)^4}\) là: \(C_4^1{.2^3}.1 = 32\)

Câu 11. Giả sử với khai triển \({(1 - 2x)^n} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_n}{x^n}\). Tìm \({a_4}\)biết \({a_0} + {a_1} + {a_2} = 31\).

A. 80. B. \( - 80\). C. 40. D. \( - 40\).

Phương pháp

Sử dụng công thức \({(1 - 2x)^n} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_n}{x^n}\)

Lời giải

Chọn A Ta có:

\({(1 - 2x)^n} = C_n^0{1^n}{( - 2x)^0} + C_n^1{n^{n - 1}}( - 2x) + C_n^2{n^{n - 2}}{( - 2x)^2} + \ldots = 1 - 2C_n^1x + 4C_n^2{x^2} + \ldots \)

Vậy \({a_0} = 1;{a_1} = - 2C_n^1;{a_2} = 4C_n^2\). Theo bài bác đi ra \({a_0} + {a_1} + {a_2} = 31\) nên tớ có:

\(1 - 2C_n^1 + 4C_n^2 = 31 \Leftrightarrow 1 - 2\frac{{n!}}{{1!(n - 1)!}} + 4\frac{{n!}}{{2!(n - 2)!}} = 31 \Leftrightarrow 1 - 2n + 2n(n - 1) = 31\)

\( \Leftrightarrow 2{n^2} - 4n - 30 = 0 \Leftrightarrow {n^2} - 2n - 15 = 0 \Rightarrow n = 5\). Từ cơ tớ với \({a_4} = C_5^4{( - 2)^4} = 80\).

Câu 12. Hình chữ nhật với những cạnh:\(x = 2m \pm 1cm\), \(y = 5m \pm 2cm\). Diện tích hình chữ nhật và sai số vô cùng của độ quý hiếm cơ là:

A. \(10{m^2}\) và \(900c{m^2}\).

B. \(10{m^2}\) và \(500c{m^2}\).

C. \(10{m^2}\) và \(400c{m^2}\).

D. \(10{m^2}\) và \(1404\;c{m^2}\).

Phương pháp

Nếu a là sai số sấp xỉ của \(\overline a \) thì \({\Delta _a} = \left| {\overline a - a} \right|\) được gọi là sai số tuyệt đối của số sấp xỉ a

Lời giải

Chọn D.

Ta với \(x = 2m \pm 1cm \Rightarrow 1,98m \le x \le 2,02m\) và \(y = 5m \pm 2cm \Rightarrow 4,98m \le nó \le 5,02m\).

Do cơ diện tích S hình chữ nhật là \(S = xy\) và \(9,8604 \le S \le 10,1404 \Rightarrow S = 10 \pm 0,1404\).

Câu 13. Một hình chữ nhật với diện tích S là \(S = 108,57c{m^2} \pm 0,06c{m^2}.\) Số những chữ số có thể của \(S\) là:

A. \(5.\) B. \(4.\) C. \(3.\) D. \(2.\)

Phương pháp

Nhắc lại khái niệm số chắc:

Trong cơ hội ghi thập phân của a, tớ bảo chữ số k cuả a là chữ số xứng đáng tin cẩn (hay chữ số chắc) nếu như sai số vô cùng ∆_a không vượt lên trước vượt một đơn vị chức năng của sản phẩm với chữ số k.

+ Ta với sai số vô cùng bởi vì \(0,06 > 0,01 \Rightarrow \)chữ số 7 là số ko có thể, \(0,06 < 0,1 \Rightarrow \)chữ số 5 là số có thể.

+ Chữ số k là số có thể thì toàn bộ những chữ số đứng phía bên trái k đều là những chữ số có thể \( \Rightarrow \) những chữ số \(1,0,8\) là những chữ số có thể. Như vậy tớ với số những chữ số có thể của \(S\)là: \(1,0,8,5.\)

Lời giải

Chọn B. Số những chữ số có thể của \(S\)là: 4

A. \(1,6\% \) B. \(1,7\% \) C. \(1,662\% \) D. \(1,66\% \)

Phương pháp

Nếu a là sai số sấp xỉ của \(\overline a \) thì \({\Delta _a} = \left| {\overline a - a} \right|\) được gọi là sai số tuyệt đối của số ngay gần đúng

+)Ta rằng a là số sấp xỉ của số chính \(\overline a \) với phỏng đúng chuẩn d nếu như \({\Delta _a} = \left| {\overline a - a} \right| \le d\) và quy ước viết lách gọn gàng là \(\overline a = a \pm d\)

+) Tỉ số \({\delta _a} = \frac{{{\Delta _a}}}{{\left| a \right|}}\) được gọi là sai số tương đối của số sấp xỉ a.

Lời giải

Chọn D

Giả sử\(a = 12 + {d_1},{\rm{ }}b = 10,2 + {d_2},{\rm{ }}c = 8 + {d_3}\).

Ta với \(P = a + b + c + {d_1} + {d_2} + {d_3} = 30,2 + {d_1} + {d_2} + {d_3}\).

Theo fake thiết, tớ có

\( - 0,2 \le {d_1} \le 0,2\, \) ;\({\rm{ }} - 0,2 \le {d_2} \le 0,2\ \) ;\( {\rm{ }} - 0,1 \le {d_3} \le 0,1\)

Suy đi ra \(--0,5 \le {d_1} + {d_2} + {d_3} \le 0,5\).

Do cơ \(P{\rm{ }} = 30,2{\rm{ cm}} \pm 0,5{\rm{ cm}}\).

Sai số vô cùng \({\Delta _P} \le 0,5\). Sai số kha khá \({\delta _P} \le \frac{d}{P} \approx 1,66\% \).

Câu 15. Số áo bán tốt nhập một quý ở cửa hàng buôn bán áo sơ-mi phái nam được tổng hợp như sau:

Cỡ áo

Tần số

(Số áo buôn bán được)

126

125

110

Giá trị kiểu mốt của bảng phân bổ tần số bên trên bằng

A. \(38\). B. \(126\). C. \(42\). D. \(12\).

Phương pháp

Mốt của kiểu số liệu là độ quý hiếm với tần số lớn số 1 nhập bảng phân bổ tần số và kí hiệu là \({M_0}\).

Lời giải

Chọn A

Vì độ quý hiếm \({x_3} = 38\) với tần số \({n_3} = 126\) lớn số 1.

A. \(6,7\) triệu đồng.

B. \(7,2\) triệu đồng.

C. \(6,8\) triệu đồng.

D. \(6,9\) triệu đồng.

Phương pháp

Sắp trật tự kiểu số liệu bao gồm n số liệu trở thành một sản phẩm ko rời ( hoặc ko tăng).

- Nếu n là lẻ thì số liệu đứng ở địa điểm loại \(\frac{{n + 1}}{2}\) ( số đứng chủ yếu giữa) gọi là trung vị

- Nếu n là chẵn thì số khoảng nằm trong của nhì số liệu đứng ở địa điểm loại \(\frac{n}{2}\) và \(\frac{n}{2} + 1\) gọi là trung vị

Lời giải

Chọn A

Sắp xếp trật tự những số liệu tổng hợp, tớ thu dược sản phẩm tăng những số liệu sau:\(2,5\);\(3,0\);\(6,5\);\(6,7\);\(6,9\);\(7,2\); \(8,4\) (đơn vị: triệu đồng).

Số trung vị \({M_e} = 6,7\) triệu đồng.

Số những số liệu tổng hợp vượt lên trước không nhiều (\(n = 7 < 10\)), vì thế ko nên lựa chọn số khoảng nằm trong thực hiện thay mặt cho những số liệu tiếp tục cho tới. Trong tình huống này tớ lựa chọn số trung vị \({M_e} = 6,7\) triệu đồng thực hiện thay mặt cho tới chi phí bổng mỗi tháng của \(7\) nhân viên cấp dưới.

Câu 17. Cho phương sai của những số liệu bởi vì \(4\). Tìm phỏng chếch chuẩn chỉnh.

A. \(4\). B. \(2\). C. \(16\). D. \(8\).

Phương pháp

Độ chếch chuẩn chỉnh là căn bậc nhì của phương sai

Lời giải

Ta có tính chếch chuẩn chỉnh là căn bậc nhì của phương sai

Nên \({s_x} = \sqrt {s_x^2} = \sqrt 4 = 2\).

Câu 18. Độ chếch chuẩn chỉnh là

A. Căn bậc nhì của phương sai.

B. Bình phương của phương sai.

C. Một nửa của phương sai.

D. Không nên những công thức bên trên.

Phương pháp

Độ chếch chuẩn chỉnh là căn bậc nhì của phương sai

Lời giải

Chọn A.Căn bậc nhì của phương sai.

Câu 19. Có 100 học viên tham gia kì thi đua học viên xuất sắc Toán (thang điểm 20). Kết trái ngược cho tới nhập bảng sau:

Khi cơ phỏng chếch chuẩn chỉnh là

A. \(1,98\). B. \(3,96\). C. \(15,23\) D. \(1,99\).

Phương pháp

Độ chếch chuẩn chỉnh là căn bậc nhì của phương sai

Lời giải

Chọn D

Ta có:

\(\overline x = \frac{{1.9 + 1.10 + 3.11 + 5.12 + 8.13 + 13.14 + 19.15 + 24.16 + 14.17 + 10.18 + 2.19}}{{100}} = 15,23\)

\(\overline {{x^2}} = \frac{{{{1.9}^2} + {{1.10}^2} + {{3.11}^2} + {{5.12}^2} + {{8.13}^2} + {{13.14}^2} + {{19.15}^2} + {{24.16}^2} + {{14.17}^2} + {{10.18}^2} + {{2.19}^2}}}{{100}} = 235,91\)

Phương sai của bảng số liệu là: \({s^2} = \overline {{x^2}} - {\left( {\overline x } \right)^2} = 235,91 - {15,23^2} = 3,9571\).

Độ chếch chuẩn chỉnh là: \(s = \sqrt {{s^2}} = \sqrt {3,9571} \approx 1,99\).

Câu trăng tròn. Điểm thi đua của lớp 10C của một ngôi trường Trung học tập Phổ Thông được trình diễn trên bảng phân bổ tần số sau:

Phương sai của bảng phân bổ tần số tiếp tục cho tới là:

A. \(0,94\) B. \(3,94.\) C. \(2,94.\) D. \(1,94.\)

Phương pháp

Cho kiểu số liêu tổng hợp với n độ quý hiếm \({x_1},{x_2},...,{x_n}\) và số khoảng nằm trong \(\overline x \).

Ta gọi số \({s^2} = \frac{{{{({x_1} - \overline x )}^2} + {{({x_2} - \overline x )}^2} + ... + {{({x_n} - \overline x )}^2}}}{n}\) là phương sai của kiểu số liệu

Lời giải

Chọn D

Trong sản phẩm số liệu về điểm thi đua của lớp 10C tớ có:

\(\overline x = \frac{1}{n} \cdot \left( {{n_1}{x_1} + {n_2}{x_2} + ... + {n_6}{x_6}} \right) = \frac{1}{{40}} \cdot \left( {7.5 + 5.6 + 10.7 + 12.8 + 4.9 + 2.10} \right) \)

\(= 7,175\)

Phương sai:

\(\begin{array}{l}{s^2} = \frac{1}{n}.\left( {{n_1}.{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}.{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_6}.{{\left( {{x_6} - \overline x } \right)}^2}} \right)\\\,\,\,\,\,\, = \frac{1}{{40}}.\left( {7.{{\left( {5 - 7,175} \right)}^2} + 5.{{\left( {6 - 7,175} \right)}^2} + 10.{{\left( {7 - 7,175} \right)}^2}} \right.\\\,\,\,\,\,\,\,\,\,\,\left. { + 12.{{\left( {8 - 7,175} \right)}^2} + 4.{{\left( {9 - 7,175} \right)}^2} + 2.{{\left( {10 - 7,175} \right)}^2}} \right)\\\,\,\,\,\,\, \approx 1,94.\end{array}\)

Câu 21. Điểm thi đua môn Toán lớp 10A₂ của một Trường trung học tập phổ thông được trình diễn trên bảng phân bổ tần số sau

Điểm thi	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)
Tần số	\(7\)	\(5\)	\(10\)	\(12\)	\(4\)	\(2\)	\(n = 40\)

Trong những độ quý hiếm sau đây, độ quý hiếm nào là sớm nhất với phương sai của bảng phân bổ tần số trên?

A. \(0,94\). B. \(3,94\). C. \(2,94\). D. \(1,94\).

Phương pháp

Cho kiểu số liêu tổng hợp với n độ quý hiếm \({x_1},{x_2},...,{x_n}\) và số khoảng nằm trong \(\overline x \).

Ta gọi số \({s^2} = \frac{{{{({x_1} - \overline x )}^2} + {{({x_2} - \overline x )}^2} + ... + {{({x_n} - \overline x )}^2}}}{n}\) là phương sai của kiểu số liệu

Lời giải

Trong sản phẩm số liệu về điểm thi đua môn Toán lớp 10A₂ tớ có

\(\overline x = \frac{1}{n}.\left( {{n_1}{x_1} + {n_2}{x_2} + ... + {n_6}{x_6}} \right) = \frac{1}{{40}}.\left( {7.5 + 5.6 + 10.7 + 12.8 + 4.9 + 2.10} \right)\)

\(= 7,175\)

Phương sai là:

A. \(A \cup B = \left\{ {SSS,\,SSN,\,NSS,\,SNS,\,NNN} \right\}\).

B. \(A \cup B = \left\{ {SSS,\,NNN} \right\}\).

C. \(A \cup B = \left\{ {SSS,\,SSN,\,NSS,\,NNN} \right\}\).

D. \(A \cup B = \Omega \).

Phương pháp

Sử dụng những quy tắc đếm

Lời giải

Chọn C

\(A = \left\{ {SSS,\,SSN,\,NSS} \right\}\), \(B = \left\{ {SSS,\,NNN} \right\}\). Suy đi ra \(A \cup B = \left\{ {SSS,\,SSN,\,NSS,\,NNN} \right\}\).

Câu 23. Gieo tình cờ một đồng xu tiền phẳng phiu và đồng hóa học \(5\) phen. Tính số thành phần không khí kiểu.

A. \(64\). B. \(10\). C. \(32\). D. \(16\).

Phương pháp

Sử dụng những quy tắc đếm

Lời giải

Chọn C

Mỗi phen gieo với nhì tài năng nên gieo 5 phen bám theo quy tắc nhân tớ với \({2^5} = 32\).

Số thành phần không khí kiểu là \(n\left( \Omega \right) = 32\).

Câu 24. Gieo một con cái súc sắc. Xác suất nhằm mặt mũi \(6\) chấm xuất hiện nay.

A. \(\frac{1}{6}\). B. \(\frac{5}{6}\). C. \(\frac{1}{2}\). D. \(\frac{1}{3}\).

Phương pháp

Sử dụng công thức tính xác suất

Lời giải

Chọn A

Gieo một con cái súc sắc với không khí kiểu \(\Omega = \left\{ {1;2;3;4;5;6} \right\} \Rightarrow n\left( \Omega \right) = 6\)

Xét đổi thay cố \(A\): “mặt \(6\) chấm xuất hiện”. \(A = \left\{ 6 \right\} \Rightarrow n\left( A \right) = 1\).

Do cơ \(P\left( A \right) = \frac{1}{6}\).

Câu 25. Gieo một con cái súc sắc phẳng phiu và đồng hóa học gấp đôi. Tính phần trăm nhằm tổng số chấm nhập nhì phen gieo nhỏ rộng lớn 6.

A. \(\frac{2}{9}\).

B. \(\frac{{11}}{{36}}\).

C. \(\frac{1}{6}\).

D. \(\frac{5}{{18}}\).

Phương pháp

Sử dụng công thức tính xác suất

Lời giải

Chọn D

Số thành phần của không khí kiểu là: \(n\left( \Omega \right) = {6^2} = 36\).

Gọi A là đổi thay cố “Tổng số chấm nhập nhì phen gieo nhỏ rộng lớn 6”.

Tập phù hợp những trái ngược của đổi thay cố A là:

\(A = \left\{ {\left( {1;1} \right);\left( {1;2} \right);\left( {1;3} \right);\left( {1;4} \right);\left( {2;1} \right);\left( {2;2} \right);\left( {2;3} \right);\left( {3;1} \right);\left( {3;2} \right);\left( {4;1} \right)} \right\}\).

Số thành phần của đổi thay cố A là: \(n\left( A \right) = 10\).

Xác suất của đổi thay cố A là: \(P\left( A \right) = \frac{{10}}{{36}} = \frac{5}{{18}}\).

A. \(e = \frac{4}{5}\). B. \(e = \frac{4}{{18}}\). C. \(e = - \frac{4}{5}\). D. \(e = \frac{4}{9}\).

Phương pháp

Tâm sai \(e = \frac{c}{a}\).

Lời giải

Chọn A

Ta với \({F_1}\left( { - 4;0} \right) \Rightarrow c = 4\).

\(\begin{array}{l}{P_{\Delta M{F_1}{F_2}}} = \underbrace {M{F_1} + M{F_2}}_{2a} + {F_1}{F_2}\\ \Leftrightarrow \,\,\,18 = 2a + 2c \Leftrightarrow 18 = 2a + 8 \Leftrightarrow a = 5.\end{array}\)

Tâm sai \(e = \frac{c}{a} = \frac{4}{5}\).

Câu 27. Trong mặt mũi bằng phẳng toạ phỏng \(Oxy\), cho tới \(\vec a = (1;2),\vec b = (3; - 3)\). Toạ phỏng của vectơ \(\vec c = 3\vec a - 2\vec b\) là:

A. \(( - 3;12)\). B. \((3;12)\). C. \((9;0)\). D. \(( - 3;0)\).

Phương pháp

Trong mặt mũi bằng phẳng \(Oxy\), cho tới \(\vec a = \left( {{a_1}\,;\,{a_2}} \right)\); \(\vec b = \left( {{b_1}\,;\,{b_2}} \right)\). Tọa phỏng vectơ \(k\overrightarrow a + t\overrightarrow b = (k{a_1} + t{b_1};k{a_2} + t{b_2})\)

Lời giải

Chọn A.

Ta có: \(3\vec a = (3;6)\) và \( - 2\vec b = ( - 6;6)\). Suy đi ra \(3\vec a - 2\vec b = ( - 3;12)\).

A. \(( - 4; - 1)\). B. \((4; - 1)\). C. \(( - 4;1)\). D. \((4;1)\).

Phương pháp

Với \(A({x_A};{y_A});B({x_B};{y_B})\) thì \(\overrightarrow {AB} = \left( {({x_B} - {x_A});({y_B} - {y_A})} \right)\)

Lời giải

Chọn\({\bf{B}}\).

Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} = (4; - 1)\)

Câu 29. Một đường thẳng liền mạch với từng nào vectơ pháp tuyến?

A. 0. B. 1. C. 2. D. Vô số.

Phương pháp

Vecto pháp tuyến có mức giá vuông góc với đường thẳng liền mạch.

Lời giải

Chọn D.

Một đường thẳng liền mạch với vô số những vecto pháp tuyến.

A. \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}\).

B. \(b\left( {x - {x_0}} \right) - a\left( {y - {y_0}} \right) = 0\).

C. \(a\left( {x + {x_0}} \right) + b\left( {y + {y_0}} \right) = 0\).

D. \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).

Phương pháp

Phương trình tổng quát lác của đường thẳng liền mạch \(\Delta \) trải qua điểm \(M\left( {{x_0};{y_0}} \right)\) và với vectơ pháp tuyến \(\vec n(a;b)\) là: \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\)

Lời giải

Chọn D

Câu 31. Đường Hyperbol \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\) với cùng 1 xài điểm là vấn đề nào là sau đây ?

A.\(\left( { - 5;0} \right)\).

B.\(\left( {0;\sqrt 7 } \right)\).

C. \(\left( {\sqrt 7 ;0} \right)\).

D. \(\left( {0;5} \right)\).

Phương pháp

Đường Hyperbol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) với xài điểm là \({F_1}\left( { - c;0} \right),{F_2}\left( {c;0} \right);\) với \(c = \sqrt {{a^2} + {b^2}} \)

Lời giải

Chọn A.

Ta với \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\) suy đi ra \(\left\{ \begin{array}{l}{a^2} = 16\\{b^2} = 9\end{array} \right. \Rightarrow {c^2} = {a^2} + {b^2} = 25 \Leftrightarrow c = 5\).

Tiêu điểm \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\).

Câu 32. Đường elip \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{7} = 1\) với xài cự bằng

A. \(3\). B. \(9\). C. \(6\). D. \(18\).

Phương pháp

Đường elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với xài cự \(2c\)với \(c = \sqrt {{a^2} - {b^2}} \)

Lời giải

Chọn C

Ta có: \({a^2} = 16\), \({b^2} = 7\) nên \({c^2} = {a^2} - {b^2} = 9\)\( \Rightarrow c = 3\).

Tiêu cự của elip là \(2c = 6\).

Câu 33. Trong mặt mũi bằng phẳng \(Oxy\), phương trình nào là sau đó là phương trình của lối tròn?

A. \({x^2} + 2{y^2} - 4x - 8y + 1 = 0\).

B. \({x^2} + {y^2} - 4x + 6y - 12 = 0\).

C. \({x^2} + {y^2} - 2x - 8y + trăng tròn = 0\).

D. \(4{x^2} + {y^2} - 10x - 6y - 2 = 0\).

Phương pháp

Phương trình lối tròn xoe (O) với tâm I(a,b) và nửa đường kính R là : \({(x - a)^2} + {(y - b)^2} = {R^2}\)

Lời giải

Chọn B

Để là phương trình lối tròn xoe thì ĐK phải là thông số của \({x^2}\) và \({y^2}\) nên đều bằng nhau nên loại được đáp án A và D.

Ta có: \({x^2} + {y^2} - 2x - 8y + trăng tròn = 0 \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 4} \right)^2} + 3 = 0\) vô lý.

Ta có:\({x^2} + {y^2} - 4x + 6y - 12 = 0 \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 25\) là phương trình lối tròn xoe tâm \(I\left( {2; - 3} \right)\), nửa đường kính \(R = 5\).

Câu 34. Trong mặt mũi bằng phẳng \(Oxy\), lối tròn xoe \(\left( C \right):{x^2} + {y^2} + 4x + 6y - 12 = 0\) với tâm là.

A. \(I\left( { - 2; - 3} \right)\).

B. \(I\left( {2;3} \right)\).

C. \(I\left( {4;6} \right)\).

D. \(I\left( { - 4; - 6} \right)\).

Phương pháp

Phương trình lối tròn xoe (O) với tâm I(a,b) và nửa đường kính R là : \({(x - a)^2} + {(y - b)^2} = {R^2}\)

Lời giải

Chọn A

Ta với phương trình lối tròn xoe là: \({\left( {x + 2} \right)^2} + {\left( {y + 3} \right)^2} = 25\).

Vậy tâm lối tròn xoe là: \(I\left( { - 2; - 3} \right)\).

A. \({\left( {x + 4} \right)^2} + {y^2} = 10\).

B. \({\left( {x - 4} \right)^2} + {y^2} = 10\).

C. \({\left( {x - 4} \right)^2} + {y^2} = \sqrt {10} \).

D. \({\left( {x + 4} \right)^2} + {y^2} = \sqrt {10} \).

Phương pháp

Phương trình lối tròn xoe với dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\,\,\left( {{a^2} + {b^2} - c > 0} \right)\). và tọa phỏng tâm \(I(a,b)\), nửa đường kính \(\,R = \sqrt {{a^2} + {b^2} - c} \)

Lời giải

Chọn B

Gọi \(I\left( {x;0} \right) \in Ox\); \(I{A^2} = I{B^2}\) \( \Leftrightarrow {\left( {1 - x} \right)^2} + {1^2} = {\left( {5 - x} \right)^2} + {3^2}\) \( \Leftrightarrow {x^2} - 2x + 1 + 1 = {x^2} - 10x + 25 + 9\) \( \Leftrightarrow x = 4\). Vậy tâm đường tròn là \(I\left( {4;0} \right)\) và bán kính \(R = IA = \sqrt {{{\left( {1 - 4} \right)}^2} + {1^2}} = \sqrt {10} \).

Phương trình đường tròn \(\left( C \right)\) có dạng \({\left( {x - 4} \right)^2} + {y^2} = 10\).

Tự luận ( 3 điểm)

a) Số học viên từng khối là bởi vì nhau?

b) Có tối thiểu 5 học viên khối \(A\) và với chính 2 học viên khối \(C\)?

Phương pháp

Sử dụng những quy tắc đếm

Lời giải:

a) Số cơ hội lựa chọn 5 học viên từng khối \((A,B,C)\) theo lần lượt là: \(C_{15}^5,C_{10}^5,C_5^5\).

Vậy số cơ hội lựa chọn vừa lòng là \(C_{15}^5 \times C_{10}^5 \times C_5^5 = 756756\) (cách).

b) Ta dùng quy tắc loại trừ như Lời giải sau:

Xét Việc 1: Chọn 2 học viên khối \(C,13\) học viên khối \(B\) hoặc khối \(A\): với \(C_5^2C_{25}^{13}\) cơ hội.

Xét Việc 2: Chọn 2 học viên khối \(C,13\) học viên khối \(B\) và khối \(A\) tuy nhiên ko vừa lòng đòi hỏi đề bài bác.

- Trường phù hợp 1: Chọn 2 học viên khối \(C,10\) học viên khối \(B\) và 3 học viên khối A với \(C_5^2C_{10}^{10}C_{15}^3\) cơ hội.

- Trường phù hợp 2: Chọn 2 học viên khối \(C,9\) học viên khối \(B\) và 4 học viên khối A với \(C_5^2C_{10}^9C_{15}^4\) cơ hội.

Vậy số cơ hội lựa chọn vừa lòng là \(C_5^2C_{25}^{13} - C_5^2C_{10}^{10}C_{15}^3 - C_5^2C_{10}^9C_{15}^4 = 51861950\) (cách).

Câu 2. Cho biểu thức \(Q = {(xy - 1)^5}\).

a) Viết khai triển biểu thức \(Q\) bởi vì nhị thức Newton.

b) Tìm số hạng với chứa chấp \({x^2}{y^2}\) nhập khai triển bên trên.

Phương pháp

Sử dụng công thức khai triển nhị thức Newton

Lời giải

a) Ta có: \(Q = {(xy - 1)^5} = C_5^0{(xy)^5} + C_5^1{(xy)^4}( - 1) + C_5^2{(xy)^3}{( - 1)^2}\)

\(\begin{array}{l} + C_5^3{(xy)^2}{( - 1)^3} + C_5^4(xy){( - 1)^4} + C_5^5{( - 1)^5}\\ = {x^5}{y^5} - 5{x^4}{y^4} + 10{x^3}{y^3} - 10{x^2}{y^2} + 5xy - 1.\end{array}\)

b) Số hạng với chứa chấp \({x^2}{y^2}\) nhập khai triển là \( - 10{x^2}{y^2}\).

80 65 51 48 45 61 30 35 84 83 60 58 75

72 68 39 41 54 61 72 75 72 61 58 65

a) Tìm phương sai và phỏng chếch chuẩn chỉnh. Nhận xét gì về những thành quả sẽ có được.

b) Tìm khoảng tầm đổi thay thiên, khoảng tầm tứ phân vị

c) Tìm độ quý hiếm bất thường

Phương pháp

a) - Cho kiểu số liêu tổng hợp với n độ quý hiếm \({x_1},{x_2},...,{x_n}\) và số khoảng nằm trong \(\overline x \).

Ta gọi số \({s^2} = \frac{{{{({x_1} - \overline x )}^2} + {{({x_2} - \overline x )}^2} + ... + {{({x_n} - \overline x )}^2}}}{n}\) là phương sai của kiểu số liệu

- Căn bậc nhì của phương sai gọi là Độ chếch chuẩn chỉnh của kiểu số liệu thống kê

b) - Ta hoàn toàn có thể tính khoảng tầm bến thiên R của kiểu số liệu bám theo công thức \(R = {x_{\max }} - {x_{\min }}\), nhập cơ \({x_{\max }}\) là độ quý hiếm lớn số 1, \({x_{\min }}\)là độ quý hiếm nhỏ nhất của kiểu số liệu cơ.

- Giả sử \({Q_1},{Q_2},{Q_3}\) là tứ phân vị của kiểu số liệu. Ta gọi hiệu \({\Delta _Q} = {Q_3} - {Q_1}\) là khoảng tầm tứ phân vị của kiểu số liệu cơ.

Lời giải

a) Tìm phương sai và phỏng chếch chuẩn chỉnh. Nhận xét gì về những thành quả sẽ có được.

Ta lập bảng phân bổ tần số như sau:

Điểm	30 35 39 41 45 48 50 51 54 58 60 61 65 68 72 75 80 83 84
Tần số	1 1 1 1 1 1 1 1 1 1 1 3 2 1 3 2 1 1 1

Ta có:

\( x = \frac{1}{n}\left( {{n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k}} \right)\\ \)

\(= \frac{1}{{25}}\left( {1.30 + 1.35 + 1.39 + 1.41 + 1.45 + 1.48 + .... + 1.60+ 3.61 + 2.65 + 1.68 + 3.72 + 2.75 + 1.80 + 1.83 + 1.84} \right)\\ = 60,\)

Phương sai:

\(s_x^2 = \frac{1}{n}\left[ {{n_1}{{({x_1} - \overline x )}^2} + {n_2}{{({x_2} - \overline x )}^2} + ... + {n_k}{{({x_k} - \overline x )}^2}} \right] = 216,8\)

Độ chếch chuẩn chỉnh \({s_x} = \sqrt {s_x^2} = \sqrt {216,8} \approx 14,724\)

Nhận xét: cường độ chênh chếch điểm trong số những độ quý hiếm là khá lớn

b) Tìm khoảng tầm đổi thay thiên, khoảng tầm tứ phân vị

Khoảng đổi thay thiên \(84 - 30 = 54\)

Nửa số liệu phía bên trái là bao gồm 12 độ quý hiếm, nhì thành phần ở trung tâm là 48,50 .

Do cơ, \({Q_1} = (48 + 50):2 = 49\).

Nửa số liệu ở bên phải là bao gồm 12 giá chỉ tri, nhì thành phần ở trung tâm là 72,72.

Do cơ, \({Q_3} = (72 + 72):2 = 72\).

Vậy khoảng tầm tứ phân vị cho tới kiểu số liệu là \({\Delta _Q} = 72 - 49 = 23\).

c) Tìm độ quý hiếm bất thường

Không có mức giá trị bất thường

Câu 4. Cho tam giác \(ABC\) với \(A( - 1; - 2)\) và phương trình đường thẳng liền mạch chứa chấp cạnh \(BC\) là \(x - nó + 4 = 0\).

a) Viết phương trình lối cao \(AH\) của tam giác.

b) Viết phương trình lối khoảng ứng với cạnh lòng \(BC\) của tam giác.

Phương pháp

Lời giải

a) Đường cao \(AH\) vuông góc với \(BC\) nên nhận \(\vec u = (1; - 1)\) thực hiện vectơ chỉ phương, suy đi ra \(AH\) với cùng 1 vectơ pháp tuyến là \(\vec n = (1;1)\).

Phương trình tổng quát lác \(AH:1(x + 1) + 1(y + 2) = 0\) hoặc \(x + nó + 3 = 0\).

b) Chọn điểm \(K(0;4)\) nằm trong \(BC\), gọi \(E\) là trung điểm đoạn \(AK\) nên \(E\left( { - \frac{1}{2};1} \right)\). Gọi \(d\) là lối khoảng ứng với cạnh lòng \(BC\) của tam giác \(ABC\), suy đi ra \(d\) qua loa \(E\) và với cùng 1 vectơ pháp tuyến .

Phương trình tổng quát lác \(d:1\left( {x + \frac{1}{2}} \right) - 1(y - 1) = 0\) hoặc \(2x - 2y + 3 = 0\).